LyX’s detailed Math manual
by the LyX Team
Version 2.0.x
1 Introduction
This document explains LyX’s math features and is furthermore a collection of LaTeX-commands used for mathematical characters and constructs. The explanations are designed for the usage of commands. It is therefore required that you have read the section Mathematical Formulas of the User’s Guide.
Most of the characters and many constructs explained in this manual are also accessible via the menu Insert ▷ Math, or the math toolbar. But everybody who has to write lots of formulas will notice that it is much faster to use commands instead of the math toolbar. Therefore this manual is focused on commands but also mentions the corresponding toolbar buttons when available.
If not specially mentioned the commands are only available within formulas. To be able to use all commands explained in this document, the option Use AMS math package must be used in the document settings (menu Document ▷ Settings ▷ Math Options).
This document doesn’t list all AmS -math commands for lucidity reasons.
2 General Instructions
To create an inline formula
↓ that is embedded into a text line, use one of the shortcuts
math-mode or the toolbar button
To create a display style formula
↓ that will appear bigger and in an own paragraph, use one of these shortcuts:
math-display.
To change a display style formula to an inline formula, set the cursor into the formula and use one of the shortcuts math-mode or the menu Edit ▷ Math ▷ Change formula type. The same way is used to change an inline formula to a display style formula.
To display parts of an inline formula in the size of a display style formula, enter the command
\displaystyle↓ to a formula. Then a new blue box appears in which the desired formula part is inserted.
Only inline formulas are allowed inside tables.
The math toolbar can be turned on in the menu View ▷ Toolbars. When you click there on “Math” the toolbar will be shown permanently at the bottom; this state is visualized in the Toolbars menu with a checkmark. When you click in this state again on “Math” in the Toolbars menu, the math toolbar is only shown when the cursor is within a formula; this state is visualized by the renaming of the menu entry from “Math” to “Math (auto)”.
The TeX-mode
↓ is invoked by pressing the toolbar button

or by using the menu
Insert ▷ TeX Code (shortcut
ert-insert).
To change the LaTeX-preamble
↓, use the menu
Document ▷ Settings ▷ LaTeX Preamble.
To edit matrices, case differentiations and multiline formulas subsequently, the menus Edit ▷ Math and Edit ▷ Rows & Columns, or the table toolbar can be used. When lines and columns are swapped via the menu, the column or line where the cursor is in is exchanged with the column to the right or the line below, respectively. Is the cursor in the last column or row, the exchange is done with the column to the left or the line above.
To write text in formulas
mathematical text↓↓ is used. This mode is invoked with the shortcut
font-default or by the insertion of the command
\text↓. The text appears black in LyX and can therefore be distinguished from the other formula parts that appear blue. In the output mathematical text is set upright, in contrary to other formula parts.
Command Scheme
Most of the LaTeX-commands for math constructs have the following scheme:
\commandname[optional argument]{required argument}
A command starts always with a backslash „
\“. To omit optional arguments, also omit the associated brackets. The braces around the required arguments are named in this document as TeX-braces
↓. If you add in a formula a left brace to a command name, LyX creates automatically a TeX-brace. In all other cases TeX-braces are created in formulas with the command
\{. TeX-braces appear red in LyX, in contrary to normal braces that appear blue. In TeX-mode no command is needed to get TeX-braces. TeX-braces don’t appear in the output.
When commands without arguments, like commands for symbols are entered in TeX-mode, a space character must always be behind the command to end it. This space doesn’t appear in the output. When the space should appear in the output, the space must be followed by a protected space in normal text.
A protected space is inserted with space-insert protected.
Syntax Explanation
-
The symbol denotes a space character to be input.
-
An arrow like → denotes the usage of the corresponding arrow key on the keyboard.
Available units
|
Unit
|
Name / Description
|
|
mm
|
Millimeter
|
|
cm
|
Centimeter
|
|
in
|
Inch (1 in = 2,54 cm)
|
|
pt
|
Point (72.27 pt = 1 in)
|
|
pc
|
Pica (1 pc = 12 pt)
|
|
sp
|
scaled point (65536 sp = 1 pt)
|
|
bp
|
big point (72 bp = 1 in)
|
|
dd
|
Didot (1 dd ≈ 0.376 mm)
|
|
cc
|
Cicero (1 cc = 12 dd)
|
|
ex
|
Height of letter “x” in the current font
|
|
em
|
width of letter “M” in the current font
|
|
mu
|
math unit (1 mu = 1⁄18 em)
|
3 Basic Functions
3.1 Exponents↓ and Indices↓↓↓
Indices are created with an underscore “_” or via the math toolbar button

, exponents with a caret “^” or via the math toolbar button

.
|
command
|
Result
|
|
B_V
|
BV
|
|
B^V
|
BV
|
|
B^ A
|
BA
|
As the caret is in some languages an accent, vowels will be accentuated in this case and not set as exponents. To get in this case exponents, press Space after the caret as in the last example.
3.2 Fractions ↓
Fractions are generated with the command
\frac↓ or via the math toolbar button
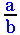
. The font size is adjusted automatically, depending on whether the fraction is in an inline or display style formula. With the math toolbar button

you can select different fraction types.
With the command
\dfrac↓ a fraction can be created that has in any case the size of a display style formula. With
\tfrac↓ the fraction appears always with the size of an inline formula. An example:
A line with the fraction (1)/(2) that was created with the command \frac.
A line with the fraction (1)/(2) that was created with the command \dfrac.
|
Command
|
Result
|
|
\frac A↓B
|
(A)/(B)
|
|
\dfrac A↓B
|
(A)/(B)
|
|
\dfrac e^ \frac 1↓2↓↓3
|
(e(1)/(2))/(3)
|
For nested fractions the command
\cfrac↓ can be used. Here is an example:
created with \frac
created with \cfrac
(A)/(B + (C + (E)/(F))/(D))
(A)/(B + (C + (E)/(F))/(D))
The command for the example above is:
\cfrac A↓B+\cfrac C+\cfrac E↓F↓D
\cfrac sets the fraction always in the size of a displayed formula, also when it is part of another fraction.
It is possible to specify the alignment of the numerator. The command \cfracleft is used to left align it, the command \cfracright to right-align it. \cfrac centers the numerator. These fractions demonstrate the different alignments:
(A)/(B + C), (A)/(B + C), (A)/(B + C)
Note: \cfracleft and \cfracright are no real LaTeX commands but represent the command \cfrac[alignment]{numerator}{denominator} . Therefore you cannot use them in TeX code.
It is often advantageous to combine
\cfrac and
\frac:
(A)/(B + (C + (E)/(F))/(D))
For inline fractions with a sloped fraction stroke you can use the command
\nicefrac↓:
5⁄31 or
\unitfrac↓:
5⁄31 There is furthermore the command
\unitfracthree that offers to write a fraction in combination with a number:
2 1⁄3
Note: \unitfracthree is not a real LaTeX command but the command
\unitfrac[number]{numerator}{denominator} . Therefore you cannot use it in TeX code.
How to define own fractions where the fraction stroke can be changed, is explained in
24.4↓.
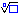
Square roots are created with
\sqrt↓ or the math toolbar button

, all other roots with the command
\root↓ or with the math toolbar button
.
|
Command
|
Result
|
|
\sqrt A-B
|
√(A − B)
|
|
\root 3↓A-B
|
3√(A − B)
|
A square root can also be created with \root when the root index field is left empty.
With certain indices the distance to the root is too small, like in this formula:
β√(B)
The
β touches the root. To avoid this, the commands
\leftroot↓ and
\uproot↓ are used with the following scheme:
\leftroot{distance} and \uproot{distance}
Distance is the number of Big Points (unit bp; 72 bp = 1 inch), that the index should be moved to the left or top, resp.. The commands are written to the index. This way the command
\root\leftroot{-1 → \uproot{2 → \beta → B
produces a correct typeset formula: β√(B)
3.4 Binomial Coefficients↓
Binomial coefficients are inserted with the command
\binom↓ or with the submenu of the math toolbar button

. Analog to fractions (
\frac) there are besides
\binom the commands
\dbinom↓ and
\tbinom↓. For other brackets around binomial coeficients there are the commands
\brace↓ and
\brack↓.
|
Command
|
Result
|
|
\binom A↓B
|
(AB)
|
|
\dbinom A↓B
|
⎛⎜⎝A B⎞⎟⎠
|
|
\tbinom A↓B
|
⎛⎜⎝A B⎞⎟⎠
|
|
\brack A↓B
|
A\brackB
|
|
\brace A↓B
|
A\braceB
|
3.5 Case Differentiations↓
|
Command
|
Result
|
|
\cases A → B>0↓
|
{
A
B > 0
|
|
\cases newline-insert newline
|
⎧⎨⎩
A
for x > 0
B
for x = 0
|
After inserting
\cases or the usage of the math toolbar button
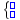
you can create new lines with the shortcut
newline-insert newline or the table toolbar button

.
The command \cases is also available via the menu Insert ▷ Math ▷ Cases-Environment.
3.6 Negations↓
By inserting of
\not↓ every character can be displayed canceled. The characters are quasi accentuated by a slash.
|
Command
|
Result
|
|
\not=
|
¬ =
|
|
\not \le
|
¬ ≤
|
|
\not \parallel
|
¬∥
|
The last example shows, that not all negations look good. Therefore there are for some negations special commands (see
13.1↓ and
14↓).
3.7 Placeholders ↓↓↓
When displaying e. g. isotopes the following problem occurs:
|
Indices created with sub- and superscripts:
|
199 F
|
|
correct indices:
|
1919 F
|
The shorter index is by default placed below or above the first character of the longer index. To avoid this there is the command
\phantom↓ or the math toolbar button

that creates one or more phantom characters. When inserting
\phantom a small blue box appears that is superposed with two red arrows. The arrows indicate that the complete width and height of the box content will be created as placeholder. Phantom characters are accordingly placeholders with the size of the characters.
|
Command
|
Result
|
|
^19 _\phantom 1 → 9 F
|
1919 F
|
|
^235 _\phantom 23 → 9 F
|
235239 F
|
|
\Lambda^ \phantom ii → t _MMt
|
ΛiitMMt
|
Furthermore there are the commands
\vphantom↓ (toolbar button

) and
\hphantom↓ (toolbar button

).
\hphantom creates only space for the maximal height of the characters in the box but not for its width.
\vphantom creates only space for the width of the box content. Therefore the boxes of both commands have only one red arrow.
For example creates
\vphantom a\int space for the height of the integral sign, because this is the larger character. An example application is in
18.1.4↓.
Placeholders can also be used for text when it is inserted via the menu Insert ▷ Formatting ▷ Phantom:
This is a sentence.
This is a sentence.
|
Command
|
Result
|
|
\overline A+B↓
|
A + B
|
|
\underline A+B↓
|
A + B
|
|
\overline \underline A+B
|
A + B
|
In the last example it doesn’t matter if first \overline or \underline is inserted.
To double underline e. g. results, one uses \underline twice.
It is possible to place up to 6 lines above or below characters.
Custom lines can be created using the command
\rule↓ which has the following scheme:
\rule[vertical offset]{length}{thickness}
The optional vertical offset shifts the line upwards (or downwards, when the value is negative). The units listed in
1↑ can be used for the values. Here are two example lines created with the commands
\rule[-2ex]{3cm}{2pt} and
\rule{2cm}{1pt}:
This is a sentence
with two lines.
\rule can also be used for text when a line is inserted via the menu Insert ▷ Formatting ▷ Horizontal Line:
This is a sentence
with one line.
3.9 Ellipses ↓
There are different types of ellipses available. For listings dots at the baseline are used (
\ldots↓), while for operations dots are needed that are on the same height as the operators (
\cdots↓). When using the command
\dots↓, LaTeX decides on the basis of the next character what type is used.
|
Command
|
Result
|
|
A_1 ,\dots ,A_n
|
A1, …, An
|
|
A_1 +\dots +A_n
|
A1 + … + An
|
|
A_1 ,\ldots ,A_n
|
A1, …, An
|
|
A_1 +\cdots +A_n
|
A1 + ⋯ + An
|
|
\vdots
|
⋮
|
|
\ddots
|
⋱
|
|
\iddots
|
\iddots
|
|
3×3 matrix with the different dots
|
A11
⋯
A1m
⋮
⋱
⋮
An1
⋯
Anm
|
The ellipses available in menu Insert ▷ Special Character are \ldots.
To use
\iddots, one of the options
Use mathdots package (automatically) must be set in the document settings under
Math Options.
Using the option
Use mathdots package will improve the appearance of all dots in the documents if their font style or size is not the default.
Specially for matrices there are ellipses that span over several columns. They are created with the command
\hdotsfor↓, that has the following scheme:
\hdotsfor[distance]{number of columns}
The number of columns specifies how many columns should be spanned. Distance is a factor for the distance between the dots.
In the following matrix the command
\hdotsfor[2]{4} was inserted in the first box of the second line, to get an ellipsis with a dot distance twice as long as with the command
\dots:
⎛⎜⎜⎜⎝
A
B
C
D
\hdotsfor[2]4
q
w
e
r
⎞⎟⎟⎟⎠
Note that the matrix fields that should be spanned must be empty, otherwise you get LaTeX-errors.
Furthermore you can fill with the command
\dotfill↓ the rest of a line with dots. The effect of these commands is the same like with
\hfill, see
8.2↓.
For example the command A\dotfill B produces
A\dotfillB
Analog to
\dotfill there is for a line the command
\hrulefill↓:
A\hrulefillB
To use the commands for text, they have to be inserted in TeX-mode.
4 Matrices ↓
Matrices can be inserted via the math toolbar button
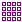
or the menu
Insert ▷ Math ▷ Matrix. In the matrix dialog you can specify the number of columns and rows, the alignment and the decoration. The vertical alignment is hereby only of importance for matrices in inline formulas:
The first matrix is top
A
D
G
J
B
E
H
K
C
F
I
L
, the second middle
A
D
G
J
B
E
H
K
C
F
I
L
and the third bottom
A
D
G
J
B
E
H
K
C
F
I
L
aligned.
The horizontal alignment specifies how the column entries should be aligned. It is set by entering a letter for every column. l denotes left aligned, c centered and r right aligned. To create for example a 4×4 matrix where the first column is left aligned, the second and third are centered and the last one is right aligned, one enters for the horizontal alignment lccr. Normally are in a matrix all columns centered, therefore the default is for every column is a c.
Horizontal alignment:
lll :
10000
D
G
B
10000
H
C
F
10000
, ccc :
10000
D
G
B
10000
H
C
F
10000
, rrr :
10000
D
G
B
10000
H
C
F
10000
To add or delete rows and columns subsequently, the math toolbar buttons

,

, etc. , or the menu
Edit ▷ Rows & Columns can be used. New rows can also be created with
newline-insert newline.
The
Decoration adds parentheses in the selected style around the matrix. Alternatively, parentheses can can either be created with the commands
\left↓ and
\right↓ (shortcut
Alt+M Parenthesis), see
5.1.2↓, or by using the following commands:
|
Command
|
Result
|
|
\bmatrix 2×2 matrix
|
0
-i
i
0
|
|
\Bmatrix 2×2 matrix
|
0
-i
i
0
|
|
\pmatrix 2×2 matrix
|
0
-i
i
0
|
|
Command
|
Result
|
|
\vmatrix 2×2 matrix
|
0
-i
i
0
|
|
\Vmatrix 2×2 matrix
|
0
-i
i
0
|
|
\matrix 2×2 matrix
|
0
-i
i
0
|
When e. g.
\vmatrix is inserted, a blue box appears between two vertical lines where the matrix is inserted.
Note that decorated matrices ignore the vertical alignment.
As all multiline formulas are matrices, the length
\arraycolsep↓ that is described in
18.1.2↓ can also be used to change the column separation of matrices.
To change the row separation, the command
\arraystretch↓ is used. It is used as follows:
\renewcommand{\arraystretch}{stretch factor}↓
The command \renewcommand assigns the stretch factor to the predefined command \arraystretch. To double e. g. the row separation, use the factor 2. This is then used for all following matrices. To go back to the original separation, assign the factor 1 to \arraystretch.
To set matrices into a text line, the command
\smallmatrix↓ is used. When it is inserted a blue box with two dashed lines appears. In this box the matrix is inserted.
This is a matrix ⎛⎜⎝
A
B
C
D
⎞⎟⎠ in a text line.
5 Brackets and Delimiters↓↓
5.1 Vertical Brackets and Delimiters↓
|
Command
|
Result
|
|
(
|
(
|
|
{
|
{
|
|
[
|
[
|
|
\langle
|
⟨
|
|
\lceil
|
⌈
|
|
\lfloor
|
⌊
|
|
/
|
⁄
|
|
|
|
|
|
|
Command
|
Result
|
|
)
|
)
|
|
}
|
}
|
|
]
|
]
|
|
\rangle
|
⟩
|
|
\rceil
|
⌉
|
|
\rfloor
|
⌋
|
|
\\
|
\
|
|
\|
|
∥
|
Note: In TeX-mode the command \textbackslash↓ must be used for the backslash, because the command \\ produces there a line break.
For all characters listed above the size can be adjusted with the commands described in the following two subsections. When using these commands, the characters < and > can directly be used instead of the commands \langle and \rangle.
5.1.1 Manual Bracket Size ↓
The bracket size can be specified manually by the LaTeX-commands
\big↓,
\Big,
\bigg and
\Bigg.
\big denotes the smallest and
\Bigg the largest bracket size.
These commands are used to emphasize levels of brackets:
|
all brackets in the same size:
|
((A + B)(A − B))C
|
|
this looks better:
|
((A + B)(A − B))C
|
For the second formula the command \Big((A+B)(A-B)\Big)^ C has been used.
Here is an overview about all bracket sizes:
\Bigg(\exp\bigg<\Big[\big{\ln(3x)\big}^2 \sin(x)\Big]^ A \bigg>\Bigg)^0,5
(exp < [{ln(3x)}2sin(x)]A > )0, 5
Besides the
\big-commands there is the variant
\bigm↓ that adds a bit more space between the bracket and its content, and the variant
\bigl-
\bigr↓, that don’t add additional space. The
l at the end of the command
\bigl is for a left bracket; for a right bracket this will be replaced by an
r. A left or right bracket can each be an opening or closing bracket.
In the following table is a comparison of the variants:
|
Command
|
Result
|
|
\Bigm(\bigm(\ln(3x)\bigm)^2 \Bigm)
|
\Bigm(\bigm(ln(3x)\bigm)2\Bigm)
|
|
\Big(\big(\ln(3x)\big)^2 \Big)
|
((ln(3x))2)
|
|
\Bigl(\bigl(\ln(3x)\bigr)^2 \Bigr)
|
\Bigl((ln(3x))2\Bigr)
|
|
\bigl)\ln(3x)\bigr(
|
)ln(3x)(
|
5.1.2 Automatic Bracket Size ↓
Brackets with variable size can be inserted with the commands
\left↓ and
\right↓ or via the math toolbar button

. Directly behind
\left and
\right the wanted bracket must be inserted. The bracket size will then automatically be calculated for the output.
normal bracket: The command
\ln(\frac A↓C ) creates
ln((A)/(C))
multiline bracket: The command
\ln\left(\frac A↓C \right) creates
ln⎛⎝(A)/(C)⎞⎠
Instead of \left and \right the shortcut Alt+M Bracket can be used. This has the advantage that you can see in LyX immediately the real bracket size and that the matching right bracket will be created too.
The command for the last example would then be: \ln Alt+M (\frac A↓C
To omit a left or right bracket, a dot is inserted for the omitted bracket. For example the command
\left.\frac A↓B \right} creates:
(A)/(B)⎫⎭
The commands
\left and
\right will be converted by LyX to brackets in the right size when the document is reloaded and an omitted bracket will appear as dashed line.
Because all popular LaTeX-Distributions use eTeX, an extension to LaTeX, the command
\middle↓ is additionally available for all brackets and limits. With this command the height of the following character is adapted to the one of the surrounding brackets, what is e. g. needed for physical vectors:
⟨φ | J = (3)/(2) , MJ⟩
For physical vectors there is a special LaTeX-package, described in
24.3↓.
5.2 Horizontal Brackets↓
|
Command
|
Result
|
|
\overbrace A+B ^ 3↓
|
A + B3
|
|
\underbrace A+B _5↓
|
A + B5
|
|
\overbrace \underbrace A+B_w _7 ^ C
|
A + Bw7C
|
In the last example it doesn’t matter if \overbrace or \underbrace is inserted at first.
When brackets are needed that overlap each other, multiline formulas, as described in
18↓, must be used:
A
=
gggg + bbqqr + dddd
gggg + bbqq + dddds
In the first row the formula is inserted together with the first brace. It is hereby important that the space command
\: is inserted before the first
d, because the brace that ends behind the
q prevents that the following “+” is surrounded by space. In the second row the second brace is inserted. As it should begin before the
b, first the command
\hphantom{gggg+\:} is inserted. This space is needed because the “+” is also surrounded by space in the formula. The brace is placed under the command
\hphantom{bbqq+dddd}.
It gets more complicated when brackets overlap each other, like in the following example:
\setlength\jot-6pt
gggg + bbqq + dddds
A
=
gggg + bbqqr + dddd
\setlength\jot3ptThe first formula row is the same as the second row of the previous example, with the difference that the brace is above. The second row contains the formula together with the second brace. To avoid that there is space between the upper brace in the first row and the formula, the row spacing need to be reduced. This is not easily possible due to a bug in LyX. As solution for the problem, the global formula row separation
\jot↓ must be changed to -6 pt before the formula with the command
\setlength{\jot}{-6pt} in TeX-mode.
\jot is set back after the formula to the standard value of 3 pt using the same command. More about the row separation in formulas is explained in
18.1.1↓.
6 Arrows↓
Arrows can be inserted via the math toolbar button
or the commands listed in the following subsections.
6.1 Horizontal Arrows↓
|
Command
|
Result
|
|
\gets
|
←
|
|
\Leftarrow
|
⇐
|
|
\longleftarrow
|
⟵
|
|
\Longleftarrow
|
⟸
|
|
\leftharpoonup
|
↼
|
|
\leftharpoondown
|
↽
|
|
\hookleftarrow
|
↩
|
|
Command
|
Result
|
|
\to
|
→
|
|
\Rightarrow
|
⇒
|
|
\longrightarrow
|
⟶
|
|
\Longrightarrow
|
⟹
|
|
\rightharpoonup
|
⇀
|
|
\rightharpoondown
|
⇁
|
|
\hookrightarrow
|
↪
|
|
Command
|
Result
|
|
\leftrightarrow
|
↔
|
|
\Leftrightarrow
|
⇔
|
|
\longleftrightarrow
|
⟷
|
|
\Longleftrightarrow
|
⟺
|
|
\rightleftharpoons
|
⇌
|
|
Command
|
Result
|
|
\mapsto
|
↦
|
|
\longmapsto
|
⟼
|
|
\leadsto
|
⇝
|
|
\dasharrow
|
\dasharrow
|
Arrows used as accent like e. g. vector arrows are listed in
7↓.
Furthermore there are the labeled arrows
↓ \xleftarrow↓ and
\xrightarrow↓. When inserting one of these commands in a formula, an arrow with two blue boxes appear where the label can be inserted. The length of the arrow adapts to the label width.
|
Command
|
Result
|
|
F(a)\xleftarrow x=a↓x>0 → F(x)
|
F(a)\xleftarrow[x > 0]x = aF(x)
|
|
F(x)\xrightarrow x=a↓x>0 → F(a)
|
F(x)\xrightarrow[x > 0]x = aF(a)
|
6.2 Vertical and diagonal Arrows↓↓
|
Command
|
Result
|
|
\uparrow
|
↑
|
|
\Uparrow
|
⇑
|
|
\updownarrow
|
↕
|
|
\Updownarrow
|
⇕
|
|
\Downarrow
|
⇓
|
|
\downarrow
|
↓
|
|
Command
|
Result
|
|
\nearrow
|
↗
|
|
\searrow
|
↘
|
|
\swarrow
|
↙
|
|
\nwarrow
|
↖
|
Vertical arrows can be used also as delimiter together with the commands described in
5.1.1↑ and
5.1.2↑.
7 Accents ↓
Accents can be inserted via the math toolbar button

or the commands listed in the following subsections.
7.1 Accents for one Character\texorpdfstring ↓
|
Command
|
Result
|
|
\dot A
|
Ȧ
|
|
\ddot A
|
Ä
|
|
\dddot A
|
A⃛
|
|
\ddddot A
|
\ddddotA
|
|
\vec A↓
|
A⃗
|
|
\bar A
|
A
|
|
\mathring A
|
Å
|
|
Command
|
Result
|
|
\tilde A
|
Ã
|
|
\hat A
|
Â
|
|
\check A
|
Ǎ
|
|
\acute A
|
Á
|
|
\grave A
|
À
|
|
\breve A
|
Ă
|
You can directly insert accents like é to formulas. LyX will transform them to the corresponding accent command. For umlauts
↓ it is better to insert a quotation mark before the vowel. These two characters are then treated by LaTeX as
one character when the formula part with the umlaut is marked as German. In contrary to
\ddot, with this method “real” umlauts are created as demonstrated in the following example:
|
Command
|
Result
|
|
“i
|
"i
|
|
\ddot i
|
ï
|
Another advantage to \ddot is that umlauts can directly be converted to mathematical text because the accent commands above are not allowed in mathematical text. To convert an accented character to mathematical text, only the character under the accent may be converted. This applies also for all other conversions, e. g. to italic or bold.
In mathematical text, umlauts and other accented characters can directly be inserted.
7.2 Accents for Operators↓
With the commands
\overset↓ and
\underset↓ characters can be placed above or below an operator, respectively, to accent it. With the command
\sideset↓ characters can be set before and behind an operator. The command scheme is:
\sideset{character before}{character behind}
\sideset must always be before the operator that should be accented. You can accent with several characters and even with other operators and symbols. To place with \sideset for example only characters behind an operator, write nothing between the first braces but don’t omit the braces.
For example the command
\sideset{ → \{’
→ \sum_k=1 ^
n produces:
\sideset’n⎲⎳k = 1
The command
\overset \maltese ↑a produces:
\overseta✠
As seen in the last example, with
\overset and
\underset also symbols and characters can be accented; with
\sideset this is not possible.
7.3 Accents for several Characters↓
|
Command
|
Result
|
|
\overleftarrow A=B
|
⟵A = B
|
|
\underleftarrow A=B
|
\underleftarrowA = B
|
|
\overleftrightarrow A=B
|
\overleftrightarrowA = B
|
|
\underleftrightarrow A=B
|
\underleftrightarrowA = B
|
|
Command
|
Result
|
|
\overrightarrow A=B
|
⟶A = B
|
|
\underrightarrow A=B
|
\underrightarrowA = B
|
|
\widetilde A=B
|
\widetildeA = B
|
|
\widehat A=B
|
^A = B
|
With these commands as many characters as you like can be accented. But the accents
\widetilde and
\widehat will only be set in the output with a length of three characters, as shown in the following example:
\widetildeA + B = C − D
With the commands
\overset↓ and
\underset↓ described in the previous subsection it is also possible to accent several characters. The command
\underset A=B↓*** creates:
\underset***A = B
8 Space ↓
8.1 Predefined Space ↓
Sometimes it is necessary to insert horizontal space to a formula. This is done by inserting a protected space (shortcut
space-insert protected). A “
” appears and by pressing
Space several times one can select one of eight different space sizes. The spaces can also be inserted using the math toolbar button

or special commands. Independent from the inserted command, one can select the size again by pressing
Space afterwards.
|
Command
|
\,
|
\:
|
\;
|
\quad
|
\qquad
|
\!
|
|
Number of Space keystrokes after inserting the protected space
|
0
|
1
|
2
|
3
|
4
|
5
|
|
Result
|
A B
|
A B
|
A B
|
A B
|
A B
|
AB
|
The last size seem to produce no space. It is displayed red in LyX contrary to the other sizes, because it is a negative space. There are two more negative spaces:
|
Command
|
\negmedspace
|
\negthickspace
|
|
Number of Space keystrokes after inserting the protected space
|
6
|
7
|
|
Result
|
A\negmedspaceB
|
A\negthickspaceB
|
Negative spaces can lead to characters overlapping each other. Thus they can be used to enforce ligatures, what is e. g. useful for summation operators:
|
Command
|
Result
|
|
\sum\sum f_kl
|
∑∑fkl
|
|
\sum\negmedspace\sum f_kl
|
∑\negmedspace∑fkl
|
Relations like for example equal signs, are always surrounded by space. To suppress this, the equal sign is placed into a TeX-brace. The following example demonstrates this:
|
normal equation
|
A = B
|
|
equation without space
|
A = B
|
The command for the last formula is: A\{= → B
Spaces are needed for physical units, because the space between the value and the unit is the smallest one and not a normal space. For units in text, the smallest space is inserted via the menu
Insert ▷ Formatting ▷ Thin Space (shortcut
space-insert thin).
An example to visualize the difference:
|
24 kW⋅h
|
space between value and unit
|
|
24 kW⋅h
|
smallest space between value and unit
|
8.2 Variable Space\texorpdfstring ↓
Space with a defined length can be inserted with the command
\hspace↓. Then a long “
” appears. The length can be specified by left-clicking on the “
”. The length may also be negative. To insert so many space that the formula uses all available space, the command
\hfill↓ is used.
|
Command (\hspace length)
|
Result
|
|
A=B\hspace → A\not=C (3 cm)
|
A = B A¬ = C
|
|
A\hspace → A\not=A (-1 mm)
|
A A¬ = A
|
|
A=A\hfill B=B
|
A = A B = B
|
In the last example the available space is given by the longest column entry of the table. In an inline formula the space depends on the length of the line in which
\hfill is inserted. Thus, when the line uses the full width, no space will be created.
\hfill only has an effect on displayed formulas when the formula style
Indented is used. (Formula styles are explained in
17↓.)
Besides
\hfill, there are the commands
\dotfill and
\hrulefill that fill the space with a pattern, see
3.9↑ for an example.
For text, variable space can be inserted via the menu Insert ▷ Formatting ▷ Horizontal Space:
This is a line with2 cm space.
This is a line with maximum space.
8.3 Space besides inline Formulas↓
The space that surrounds inline formulas can be adjusted with the length
\mathsurround↓. The value of a length is set with the command
\setlength↓ that has the following scheme:
\setlength{length name}{value}
To set \mathsurround to the value 5 mm, the command
\setlength{\mathsurround}{5mm}
is inserted in TeX-mode. 5 mm space will now be set around all inline formulas:\setlength\mathsurround5mm
This is a line with an inline formula A = B with 5 mm surrounding space.\setlength\mathsurround0pt
To return to the predefined value, \mathsurround is set to the value 0 pt.
9 Boxes and Frames↓↓
Boxes for text are described in chapter Boxes in the Embedded Objects manual.
9.1 Boxes with Frame ↓
It is possible to frame formulas or parts of it with the commands
\fbox↓ and
\boxed↓.
When one of these commands is inserted to a formula, a blue box appears within a frame to enter formula parts. For \fbox an additional formula has to be created by Ctrl+M within this box, because the box content will otherwise be treated as mathematical text. When \boxed is used, a new formula is automatically created inside the frame.
The command \fbox is not suitable to frame displayed formulas because the formula will always be set in the size of the text. \boxed is in contrary not suitable to frame inline formulas, because the formula will always be set in the size of a displayed formula.
As extension to
\fbox there is the command
\framebox↓ where additionally the frame width and the alignment can be specified.
\framebox is used in the following scheme:
\framebox[frame width][position]{box content}
The position can either be l or r. l left aligns, r right aligns the formula in the box. When no position is given, the formula will be centered.
Is no width given, also no position can be given. In this case the frame width is adjusted to the box content like for \fbox.
When the command \framebox is inserted, a box appears containing three blue boxes. The first two boxes are surrounded by brackets and denote the two optional arguments. The third box is for formula parts like for \fbox.
|
Command
|
Result
|
|
\fbox Ctrl+M \int A=B
|
∫A = B
|
|
\boxed \int A=B
|
∫A = B
|
|
A+\fbox B
|
A + B
|
|
\framebox 20mm → → Ctrl+M \frac A↓B
|
(A)/(B)
|
The frame thickness can also be adjusted. To do this the following commands have to be inserted in TeX-mode before the formula
\fboxrule “thickness” \fboxsep “distance”
“distance” specifies the minimal distance between the frame and the first character in the box. An example for this is the following framed formula:
A + B = C
Before this formula the commands
\fboxrule 2mm \fboxsep 3mm
were inserted in TeX-mode. The given values are used for all following boxes.
To return to the standard frame size, the command
\fboxrule 0.4pt \fboxsep 3pt
is inserted in TeX-mode before the next formula.
9.2 Boxes without Frame ↓
For boxes without a frame there are the following box commands:
\mbox↓,
\makebox↓ and
\raisebox↓
With \raisebox a box can be super- or subscripted. But in contrary to normal super- and subscripting, the characters in the box keep their font size. \raisebox is used in the following scheme:
\raisebox{height}{box content}
When the box should contain a formula, an extra formula is needed like for \fbox.
Note: For \raisebox this extra formula is created by pressing Ctrl+M twice instead of once because LyX doesn’t yet support \raisebox directly.
|
Command
|
Result
|
|
H\raisebox{2mm → \{al → lo
|
Hallo
|
|
H\raisebox{-2mm → \{al → lo
|
Hallo
|
|
A=\raisebox{-2mm → \{Ctrl+M Ctrl+M \sqrt B
|
A = √(B)
|
The command \mbox is equivalent to \fbox and \makebox is equivalent to \framebox, with the difference that there is no frame.
9.3 Colored Boxes ↓
To be able to use all commands explained in this section, the LaTeX-package
color↓ has to be loaded in the LaTeX-preamble with the line
\usepackage{color}
To color boxes, the command
\colorbox↓ is used in the following scheme:
\colorbox{color}{box content}
The box content can also be a box and a \colorbox can also be part of another box (see the 2nd and 3rd example). When the box should contain a formula, an extra formula has to be created, the same way as for \raisebox.
One of the following predefined colors can be chosen:
black, blue, cyan, green, magenta, red, white and yellow
|
Command
|
Result
|
|
\colorbox{yellow → \{A=B
|
A = B
|
|
\colorbox{green → \{\fbox A=B
|
A = B
|
|
\fbox \colorbox{green → \{Ctrl+M Ctrl+M \int C=D
|
∫C = D
|
\colorbox only colors the box but not the characters in the box. To color all characters, the whole formula is highlighted and the wanted color is chosen in the
Text Style dialog. The dialog can be called with the toolbar button
or the menu
Edit ▷ Text Style ▷ Customized. The formula number has then the same color as the formula. When the formula number should get another color than the formula characters, the color must be changed within the formula.
An example:
Formula
(1↑) is completely colored red.
Formula
(2↑) was first completely colored green to set the color for the formula number. Subsequently the formula characters were colored red.
To color the frame different than the rest of the box, the command
\fcolorbox↓ is used in the following scheme:
\fcolorbox{frame color}{color}{box content}
So
\fcolorbox is an extension of the command
\colorbox. The frame width is set, like for
\framebox, with
\fboxrule and
\fboxsep. An example:
A = B
This formula was created with the command
\fcolorbox{cyan → \{magenta → \{A=B.
To use other colors than the predefined ones, they have to be defined first.
One can for example define the color “darkgreen” with the LaTeX-preamble line:
\definecolor{darkgreen}{cmyk}{0.5, 0, 1, 0.5}↓
cmyk is the color space that denotes the colors cyan, magenta, yellow and black. The four comma separated numbers are the portion factor for the corresponding colors of the color space. The factors can be in the range of 0 - 1. Instead of cmyk also the color space rgb can be used for definitions. rgb denotes red, green and blue, so that there are in this case three portion factors for the corresponding colors. Furthermore there is the color space gray with one portion factor for the gray value.
As example a framed box with the new defined color
darkgreen where the characters have been colored
yellow:
Self-defined colors can also be used for text with the help of the command
\textcolor:
↓
This sentence is “darkgreen”.
\textcolor↓ is used in the scheme
\textcolor{color}{characters to color}.
9.4 Paragraph Boxes ↓
A box that can contain several lines and paragraphs, a so called paragraph box (parbox), can be created with the menu
Insert ▷ Box or the toolbar button

.
The following example shows a framed parbox in a line:
This is a line
This is a paragraph box. It is exactly 5 cm long and can also contain formulas: ∫A ds = C
with a parbox.
Such a box is created by right-clicking on the gray box inset. A dialog pops up showing the box properties. In our case set: Decoration: Recangular box, Inner Box: Parbox, Width: 5 cm, Vertical Box Alignment: Middle
In LaTeX a parbox is created with the command
\parbox↓ that has the following scheme:
\parbox[position]{width}{box content}
The positions b and t are possible. b for bottom means that the box is aligned within the surrounding text with its last line. With t for top this is done with the first line. When no position is given, the box will be vertically centered, see section Boxes of the Embedded Objects manual for examples.
To frame formulas completely, including the formula number, the formula must be set into a parbox. To do this, the command
\fbox{\parbox{\linewidth-2\fboxsep-2\fboxrule}{ is inserted in TeX-mode before the formula.
\linewidth↓ is hereby the line width set for the document. Because the frame is outside the parbox, 2 times the frame separation and the frame thickness must be subtracted from the line width. As this is not automatically done by LyX due to a bug, TeX-mode has to be used. To be able to multiply and subtract in arguments, the LaTeX-package
calc↓ must be loaded in the LaTeX-preamble with the line
\usepackage{calc}
Behind the formula both boxes are closed by entering }} in TeX-mode. Here is an example:
As a parbox is used as argument of
\fbox, there is in this case no difference between
\fbox and
\boxed.
Paragraph boxes are very useful to comment formulas directly. To do this,
\parbox is used in combination with the command
\tag. (more about
\tag see
19.4↓)
An example of a formula commented with \parbox:
5x − 7b = 3b
This is a description. It is distinctly separated from the formula and multiline.
\]
Such a formula must be inserted completely in TeX-mode because LyX does not yet support the command \parbox in formulas. The formula is created with the following command sequence:
The command \[5x-7b=3b\tag*\{\parbox{5cm}{ is inserted in TeX-mode. Then the description follows as normal text and finally }}\] is inserted in TeX-mode. The commands \[ and \] hereby create a displayed formula.
The advantages of
\parbox can be seen in this example that was “commented” using the mathematical textmode:
5x − 7b = 3bThis is a description. It is not separated from the formula ...
10 Operators↓
10.1 Big Operators ↓↓↓
To be able to use all integral operators listed here, the option Use esint package automatically must be set in the document settings under Math Options.
|
Command
|
Result
|
|
\int↓
|
∫
|
|
\oint
|
∮
|
|
\ointctrclockwise
|
∳
|
|
\ointclockwise
|
∲
|
|
\sqint
|
\sqint
|
|
\fint
|
\fint
|
|
\landupint
|
∱
|
|
\landdownint
|
\landdownint
|
|
\bigcap
|
∩
|
|
\bigcup
|
∪
|
|
Command
|
Result
|
|
\sum↓
|
∑
|
|
\prod↓
|
∏
|
|
\coprod
|
∐
|
|
\bigodot
|
⊙
|
|
\bigotimes
|
⊗
|
|
\bigoplus
|
⊕
|
|
\bigwedge
|
∧
|
|
\bigvee
|
∨
|
|
\bigsqcup
|
⊔
|
|
\biguplus
|
⊎
|
All big operators can also be inserted via the math toolbar button
.
The operators are called big because they are bigger than the sometimes equal looking binary operators. All big operators can have limits as described in the next subsection.
For all integral operators there is a second version available, ending on
op:
\intop,
\ointop etc.. These operators are different from
\int etc. in the style the operator limits are displayed, see
10.2↓.
Advice for Integrals
The letter d in an integral is an operator, that therefore has to be set upright. This is done by highlighting the d and using the keyboard shortcut font-roman. Finally the smallest space is inserted before the d, as this is usual for operators. An example:
incorrect: ∫A(x)dx
incorrect: ∫A(x) dx
For multiple integrals there are the following commands:
|
Command
|
Result
|
|
\iint
|
∬
|
|
\oiint
|
∯
|
|
\sqiint
|
\sqiint
|
|
Command
|
Result
|
|
\iiint
|
∭
|
|
\iiiint
|
\iiiint
|
|
\dotsint
|
\dotsint
|
10.2 Operator Limits ↓
Limits are created by super- and subscripts:
|
Command
|
Result
|
|
\prod^\infty → _0 → A(x)
|
∏∞0A(x)
|
Limits of inline formulas are set right beside the operator. Limits in displayed formulas are set above or below the operator, except for integral limits.
To force that the limits are set beside the operator, the cursor is set directly behind the operator and the limits type is changed with the menu Edit ▷ Math ▷ Change Limits Type to Inline (shortcut math-limits). An example:
The default limits type is this:
∞⎲⎳x = 0(1)/(x2)
This is how it looks when the limits type was changed to
Inline:
⎲⎳∞x = 0(1)/(x2)
For integrals, except those ending with
op like
\intop,
\ointop etc., the limits are by default set beside the operator. But for multiple integrals the limits are often set below the operator. In the following example the limits type was therefore set to
Display and so set below the integrals:
To specify conditions for limits, the commands
\subarray↓ and
\substack↓ are used. To create for example this expression
the following has to be done:
First the command \sum^n _ is typed in. One is now in a blue box under the summation operator and insert there the command \subarray . The blue box is now within a purple box and now several lines can be written among each other. A new line is created by inserting a line break (newline-insert newline). When now
0<k<1000 Ctrl+Return
is typed in, a new box appears below for the new line.
The alignment of the lines can be changed to left aligned with the table toolbar or the menu Edit ▷ Rows &Columns. To get right alignment, \hfill is inserted at the beginning of the line.
The command \substack is equivalent to \subarray with the difference that the lines are always centered.
Like in formula
(6↑) there can be too much space beside an operator, because the characters following the operator are set beside the limits.
To avoid this, the following macro can be used in the LaTeX-preamble:
\def\clap#1{\hbox to 0pt{\hss #1\hss}}
\def\mathclap {\mathpalette \mathclapinternal}
\def\mathclapinternal #1#2{\clap{$\mathsurround =0pt #1{#2}$}}
This defines the command
\mathclap↓ that sets the width of the limit to 0 pt. The command scheme is
\mathclap{limit}
where the limit can consist of several conditions.
Applied on formula
(6↑), one uses the command
\sum_\mathclap{\substack 0<k<1000 Ctrl+Return
to create the lower limit. The summand is now directly behind the summation operator:
n⎲⎳\mathclap\substack0 < k < 1000
k ∈ ℕk − 2
How to use one limit for several operators is described in
10.4↓.
10.3 Binary Operators ↓
Binary operators are surrounded by space when there is a character before and behind them.
|
Command
|
Result
|
|
+
|
+
|
|
-
|
−
|
|
\pm
|
±
|
|
\mp
|
∓
|
|
\cdot
|
⋅
|
|
\times
|
×
|
|
\div
|
÷
|
|
*
|
*
|
|
\star
|
⋆
|
|
\circ
|
○
|
|
\diamond
|
◇
|
|
\bullet
|
•
|
|
Command
|
Result
|
|
\nabla
|
∇
|
|
\bigtriangledown
|
▽
|
|
\bigtriangleup
|
△
|
|
\Box
|
□
|
|
\cap
|
∩
|
|
\cup
|
∪
|
|
\dagger
|
†
|
|
\ddagger
|
‡
|
|
\wr
|
≀
|
|
\bigcirc
|
○
|
|
\wedge
|
∧
|
|
\vee
|
∨
|
|
Command
|
Result
|
|
\oplus
|
⊕
|
|
\ominus
|
⊖
|
|
\otimes
|
⊗
|
|
\oslash
|
⊘
|
|
\odot
|
⊙
|
|
\amalg
|
∐
|
|
\uplus
|
⊎
|
|
\setminus
|
∖
|
|
\sqcap
|
⊓
|
|
\sqcup
|
⊔
|
|
\triangleleft
|
⊲
|
|
\triangleright
|
▷
|
All binary operators can also be inserted via the math toolbar button
.
To typeset the Laplace operator also \Delta or \nabla^2 (∇2) can be used instead of \bigtriangleup .
The character Menu Separator from the menu Insert ▷ Special Character is the operator \triangleright.
10.4 Self-defined Operators ↓
With the help of the command
\DeclareMathOperator↓ custom operators can be defined in the LaTeX-preamble. Its command scheme is:
\DeclareMathOperator{new command}{display}
Display can be characters or symbols that define how the operator looks in the output. To define a big operator a * is set behind the command. All self-defined big operators can have limits as described in
10.2↑.
For example the LaTeX-preamble line
\DeclareMathOperator*{\Lozenge}{\blacklozenge}
defines the command
\Lozenge, that inserts a big operator consisting of the lozenge symbol from
13.2↓:
\Lozenge∞n = 1
The command for this formula is:
\Lozenge^
\infty → _n=1
When self-defined operators are not used several times in the document, they can also be defined with the commands
\mathop↓ and
\mathbin↓, which have the following scheme:
\mathop{display} and \mathbin{display}
\mathop defines big operators, \mathbin binary operators.
\mathop can e. g. be used to use one limit for several operators:
\mathop⎲⎳\negmedspace⎲⎳Ni, j = 1
The command for the formula above is:
\mathop{\sum\negmedspace\sum → ^N _i,j=1
11.1 Font Styles ↓
Latin letters in formulas can be set in one of the following font styles:
|
Command
|
Result
|
shortcut
|
|
\mathbb ABC
|
ABC
|
font-noun
|
|
\mathbf AbC
|
AbC
|
font-bold
|
|
\boldsymbol AbC
|
AbC
|
font-boldsymbol
|
|
\mathcal ABC
|
ABC
|
font-emph
|
|
\mathfrak AbC
|
AbC
|
-
|
|
\mathscr AbC
|
AbC
|
-
|
|
Command
|
Result
|
shortcut
|
|
\mathit AbC
|
AbC
|
-
|
|
\mathrm AbC
|
AbC
|
font-roman
|
|
\mathsf AbC
|
AbC
|
font-sans
|
|
\mathtt AbC
|
AbC
|
font-typewriter
|
Note: The styles \mathbb and \mathcal can only be used for big letters.
Predefined is the style \mathnormal.
The style commands work also for letters in mathematical constructs:
A = (b)/(C)
Characters in mathematical text don’t appear in a math font style but in the text font style \textrm. That their style can’t be set correctly via the text style dialog is a bug in LyX.
Instead of the style commands the dialog
Edit ▷ Math ▷ Text Style or the toolbar button

can be used.
11.2 Bold Formulas ↓
To make a complete formula bold, the command \mathbf from the previous subsection cannot be used, because it doesn’t work for small Greek letters. Furthermore it prints Latin letters always upright, like in the following equation:
2⌠⌡nf(θ) = Γ equation with \mathbf
To display the formula correctly, the command
\boldsymbol is used:
2⌠⌡nf(θ) = Γ equation with \boldsymbol
It is also possible to set the formula in a
boldmath environment. This environment is created by inserting the command
\boldmath↓ in TeX-mode. To end the environment, the command
\unboldmath↓ is inserted in TeX-mode.
\boldmath
2⌠⌡nf(θ) = Γ equation in a boldmath environment
\unboldmath
11.3 Colored Formulas↓
Formulas can be colored like normal text: Highlight a formula or a formula part and use the
Text Style dialog. Here is a formula in magenta:
⌠⌡A dx = (5√(B))/(ln⎛⎝(1)/(3)⎞⎠)
You can also define your own colors as described in
9.3↑. They can be used with the TeX code command
\textcolor↓ in the scheme
\textcolor{color}{characters or formula}
The following example was colored completely dark green and partly red:
⌠⌡A dx = (5√(B))/(ln⎛⎝(1)/(3)⎞⎠)
Due to a bug in LyX only complete formulas can be colored with self-defined colors.
11.4 Font Sizes ↓
For characters in formulas there are, analog to characters in text, the following size commands:
\Huge, \huge, \LARGE, \Large, \large, \normalsize, \small,
\footnotesize, \scriptsize and \tiny
The size produced by the commands depends on the document font size, that corresponds with the command \normalsize. The other commands produce smaller or larger sizes than \normalsize. The font size can however not exceed a certain value. Is for example the document font size 12 pt, the command \Huge switches to the same size as \huge.
A size command is inserted in TeX-mode before the formula and sets the size for all following formula and text characters. To switch back to the initial size, the command \normalsize is inserted behind the formula in TeX-mode.
Within a formula the size can be changed using the following size commands:
|
Command
|
Result
|
|
\displaystyle↓
|
Epot1 = (K)/(l + (m)/(n2))
|
|
\textstyle
|
Epot1 = (K)/(l + (m)/(n2))
|
|
\scriptstyle
|
Epot1 = (K)/(l + (m)/(n2))
|
|
\scriptscriptstyle
|
Epot1 = (K)/(l + (m)/(n2))
|
After entering these commands, a blue box appears in which the formula parts are inserted.
There is a further method to change the font size, that though only works for symbols or letters in mathematical text. To use it, one of the above text size commands is inserted in mathematical text. All following characters until the end of the mathematical text or until another size command will have the selected size. Two examples:
\huge
A = (B)/(c)⋅✠
✠A\Large✠A\tiny✠A
\normalsize
Before both formulas the command
\huge was inserted. The command for the second formula is:
\maltese A Alt+M M \Large \maltese \textit A → →
Alt+M M \tiny \maltese \textit A
If a symbol cannot be displayed in different sizes, it will always be displayed in the default size.
12 Greek Letters↓
Greek letters can also be inserted via the toolbar button
. All international typesetting norms purport that Greek letters in math have to be typeset italic/slanted. In some languages, like French or Russian, they are nevertheless sometimes typeset upright.
12.1 Small Letters↓
|
Command
|
Result
|
|
\alpha
|
α
|
|
\beta
|
β
|
|
\gamma
|
γ
|
|
\delta
|
δ
|
|
\epsilon
|
ϵ
|
|
\varepsilon
|
ε
|
|
\zeta
|
ζ
|
|
\eta
|
η
|
|
\theta
|
θ
|
|
\vartheta
|
ϑ
|
|
Command
|
Result
|
|
\iota
|
ι
|
|
\kappa
|
κ
|
|
\varkappa
|
ϰ
|
|
\lambda
|
λ
|
|
\mu
|
μ
|
|
\nu
|
ν
|
|
\xi
|
ξ
|
|
o
|
o
|
|
\pi
|
π
|
|
\varpi
|
ϖ
|
|
\rho
|
ρ
|
|
Command
|
Result
|
|
\varrho
|
ϱ
|
|
\sigma
|
σ
|
|
\varsigma
|
ς
|
|
\tau
|
τ
|
|
\upsilon
|
υ
|
|
\phi
|
φ
|
|
\varphi
|
φ
|
|
\chi
|
χ
|
|
\psi
|
ψ
|
|
\omega
|
ω
|
How to create special upright Greek letters is explained in
24.9↓.
12.2 Big Letters↓
|
Command
|
Result
|
|
\Gamma
|
Γ
|
|
\Delta
|
Δ
|
|
\Theta
|
Θ
|
|
\Lambda
|
Λ
|
|
\Xi
|
Ξ
|
|
\Pi
|
Π
|
|
Command
|
Result
|
|
\Sigma
|
Σ
|
|
\Upsilon
|
Υ
|
|
\Phi
|
Φ
|
|
\Psi
|
Ψ
|
|
\Omega
|
Ω
|
That the big Greek letters appear upright is caused by a design bug when TeX was developed. To get correct italic big letters, begin every command with
var. For example the command
\varGamma produces
Γ. Another way is to load the package
fixmath↓ with the LaTeX-preamble line
\usepackage{fixmath}
Then all big Greek letters in a document will automatically be typeset italic.
12.3 Bold Letters↓
Greek letters cannot be set with different font styles like Latin letters. They can only be made bold with the command
\boldsymbol↓.
|
Command
|
Result
|
|
\Upsilon\boldsymbol\Upsilon
|
ΥΥ
|
|
\theta\boldsymbol\theta
|
θθ
|
13 Symbols\texorpdfstring↓
Many of the symbols listed in this section can also be inserted via the toolbar buttons
and
.
13.1 Mathematical Symbols ↓
|
Command
|
Result
|
|
\neg
|
¬
|
|
\Im
|
ℑ
|
|
\Re
|
ℜ
|
|
\aleph
|
ℵ
|
|
\partial
|
∂
|
|
\infty
|
∞
|
|
\wp
|
℘
|
|
\imath
|
ı
|
|
\jmath
|
ȷ
|
|
Command
|
Result
|
|
\forall
|
∀
|
|
\exists
|
∃
|
|
\nexists
|
∄
|
|
\emptyset
|
∅
|
|
\varnothing
|
∅
|
|
\dag
|
†
|
|
\ddag
|
‡
|
|
\complement
|
∁
|
|
\Bbbk
|
\Bbbk
|
|
Command
|
Result
|
|
\prime
|
′
|
|
\backprime
|
‵
|
|
\mho
|
℧
|
|
\triangle
|
△
|
|
\angle
|
∠
|
|
\measuredangle
|
∡
|
|
\sphericalangle
|
∢
|
|
\top
|
⊤
|
|
\bot
|
⊥
|
13.2 Miscellaneous Symbols ↓
|
Command
|
Result
|
|
\flat
|
♭
|
|
\natural
|
♮
|
|
\sharp
|
♯
|
|
\surd
|
√
|
|
\checkmark
|
✓
|
|
\yen
|
¥
|
|
\pounds
|
£
|
|
$
|
$
|
|
§
|
§
|
|
Command
|
Result
|
|
\hbar
|
ℏ
|
|
\hslash
|
ℏ
|
|
\clubsuit
|
♣
|
|
\spadesuit
|
♠
|
|
\bigstar
|
★
|
|
\blacklozenge
|
⧫
|
|
\blacktriangle
|
▲
|
|
\blacktiangledown
|
▼
|
|
\bullet
|
•
|
|
Command
|
Result
|
|
\diamondsuit
|
♦
|
|
\Diamond
|
◇
|
|
\heartsuit
|
♥
|
|
\P
|
¶
|
|
\copyright
|
©
|
|
\circledR
|
®
|
|
\maltese
|
✠
|
|
\diagup
|
╱
|
|
\diagdown
|
╲
|
More symbols are listed in
16.4↓.
Some symbols can be displayed in different sizes, see
11.4↑.
13.3 The Euro-Symbol €↓↓
To use the Euro symbol in formulas, the LaTeX-package
eurosym↓ must be installed and loaded with the LaTeX-preamble line
\usepackage[gennarrow]{eurosym}
The Euro symbol can now be inserted with the command
\euro↓.
The Euro symbol can directly be inserted with the € key in mathematical text, without having
eurosym installed. When
eurosym is installed,
\euro can also be inserted in TeX-mode. The official currency symbol can then be inserted with the command
\officialeuro↓, that is only available in TeX-mode.
\ifeurosym
An overview about the different Euro symbols:
|
|
Command
|
Result
|
|
formula
|
\euro
|
€
|
|
mathematical text
|
€
|
€
|
|
TeX-mode
|
\officialeuro
|
€
|
\else
You need to install the LaTeX-package eurosym to see the rest of this subsection in the output.
\fi
14 Relations ↓↓
All relations can also be inserted via the toolbar button
.
|
Command
|
Result
|
|
<
|
<
|
|
\le
|
≤
|
|
\ll
|
≪
|
|
\prec
|
≺
|
|
\preceq
|
≼
|
|
\subset
|
⊂
|
|
\subseteq
|
⊆
|
|
\sqsubseteq
|
⊑
|
|
\in
|
∈
|
|
\vdash
|
⊢
|
|
\smile
|
⌣
|
|
\lhd
|
⊲
|
|
\unlhd
|
⊴
|
|
\gtrless
|
≷
|
|
\mid
|
∣
|
|
\nmid
|
∤
|
|
Command
|
Result
|
|
=
|
=
|
|
\not=
|
¬ =
|
|
\equiv
|
≡
|
|
\sim
|
~
|
|
\simeq
|
≃
|
|
\approx
|
≈
|
|
\cong
|
≅
|
|
\bowtie
|
⋈
|
|
\notin
|
∉
|
|
\perp
|
⊥
|
|
\propto
|
∝
|
|
\asymp
|
≍
|
|
\doteq
|
≐
|
|
\circeq
|
≗
|
|
\models
|
⊨
|
|
\widehat=
|
^ =
|
|
Command
|
Result
|
|
>
|
>
|
|
\ge
|
≥
|
|
\gg
|
≫
|
|
\succ
|
≻
|
|
\succeq
|
≽
|
|
\supset
|
⊃
|
|
\supseteq
|
⊇
|
|
\sqsupseteq
|
⊒
|
|
\ni
|
∋
|
|
\dashv
|
⊣
|
|
\frown
|
⌢
|
|
\rhd
|
⊳
|
|
\unrhd
|
⊵
|
|
\lessgtr
|
≶
|
|
\parallel
|
∥
|
|
\nparallel
|
∦
|
The characters
\lhd and
\rhd are bigger than the equal looking operators
\triangleleft and
\triangleright, respectively.
Relations are, in contrary to symbols, always surrounded by space.
Relations with labels can be created with the command
\stackrel↓:
|
Command
|
Result
|
|
A(r)\stackrel r\to\infty ↓\approx B
|
A(r)r → ∞ ≈ B
|
15 Functions
15.1 Predefined Functions ↓
In general, variables are set italic in mathematical expressions, but not function names, because sin could be misunderstood as s⋅i⋅n. Therefore there are predefined functions, that are additionally a bit separated from prefactors. They are inserted as commands starting with a backslash before their name.
|
Command
|
Result
|
Command
|
Result
|
|
Asin(x)+B
|
Asin(x) + B
|
A\sin(x)+B
|
Asin(x) + B
|
The following functions are predefined:
|
Command
|
Command
|
Command
|
Command
|
|
\sin
|
\sinh
|
\arcsin
|
\sup
|
|
\cos
|
\cosh
|
\arccos
|
\inf
|
|
\tan
|
\tanh
|
\arctan
|
\lim
|
|
\cot
|
\coth
|
\arg
|
\liminf
|
|
\sec
|
\min
|
\deg
|
\limsup
|
|
\csc
|
\max
|
\det
|
\Pr
|
|
\ln
|
\exp
|
\dim
|
\hom
|
|
\lg
|
\log
|
\ker
|
\gcd
|
They can also be inserted with the math toolbar button
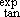
.
15.2 Self-defined Functions↓
To use a function that is not predefined, like for example the sign function sgn(x), there are two possibilities:
-
Define the function by inserting the following line to the LaTeX-preamble
\DeclareMathOperator{\sgn}{sgn}↓
Now the new defined function can be called with the command \sgn.
-
Write the formula as usual, mark the formula name, in our example the letters sgn, and change it to mathematical text. At last a space is inserted between prefactor and function.
The result is the same with both methods as with a predefined function:
|
Command
|
Result
|
|
A\sgn(x)+B
|
A\sgn(x) + B
|
|
A\,sgnAlt+M M(x)+B
|
A sgn(x) + B
|
The first method is more suitable when the self-defined function should be used several times.
For limits there are defined besides
\lim↓,
\liminf and
\limsup furthermore the following functions:
|
Command
|
Result
|
|
\varliminf
|
\varliminf
|
|
\varlimsup
|
\varlimsup
|
|
\varprojlim
|
\varprojlim
|
|
\varinjlim
|
\varinjlim
|
The limit is created by inserting a subscript. It is set right beside the function in an inline formula:
|
Command
|
Result
|
|
\lim_x\to A x=B
|
limx → Ax = B
|
In a displayed formula the limit is set below the formula, as usual:
limx → Ax = B
15.4 Modulo-Functions↓
The modulo-function is special, because it exists in four variants.
The variants in a displayed formula:
Command
Result
a\mod b
a\modb
a\pmod b
a\pmodb
a\bmod b
a\bmodb
a\pod b
a\podb
In an inline formula less space is set before the function names for all variants.
16 Special Characters↓
16.1 Special Characters in Mathematical Text
The following commands can only be used in mathematical text or in TeX-mode:
|
Command
|
Result
|
|
\oe
|
œ
|
|
\OE
|
Œ
|
|
\ae
|
æ
|
|
\AE
|
Æ
|
|
\aa
|
å
|
|
\AA↓
|
Å
|
|
\i
|
ı
|
|
command
|
Result
|
|
\o
|
ø
|
|
\O
|
Ø
|
|
\l
|
ł
|
|
\L
|
Ł
|
|
!‘
|
!`
|
|
?‘
|
?`
|
|
\j
|
ȷ
|
The characters
Å and
Ø can also be inserted via the math toolbar button
.
An exception are the commands !‘ and ?‘, because they can be inserted in LyX directly to text.
16.2 Accents in Text ↓
With the following commands all letters can be accented. The commands must be inserted in TeX-mode.
|
Command
|
Result
|
|
\“e
|
ë
|
|
\‘e
|
\‘e
|
|
\^ e
|
ê
|
|
\=e
|
\=e
|
|
\u e
|
\u e
|
|
\b e
|
\b e
|
|
\t ee
|
\t ee
|
|
Command
|
Result
|
|
\H e
|
\H e
|
|
\’e
|
\’e
|
|
\~e↓
|
ẽ
|
|
\.e
|
\.e
|
|
\v e
|
\v e
|
|
\d e
|
\d e
|
|
\c e
|
ȩ
|
With the command
\t also two different characters can be accented. The command
\t sz creates:
\t sz
The accents ‘ , ’ and ^ can in combination with vowels directly be inserted with the keyboard without using TeX-mode. The same applies for the tilde ~ in combination with a , n , or o.
The commands
\b ,
\c ,
\d ,
\H ,
\t ,
\u ,
\v and accents that are inserted directly with the keyboard are also available in mathematical text. For the other accents there are special math commands to be used in formulas, see
7.1↑.
Furthermore, with the command
\textcircled↓ all numbers and letters can be set into a circle, quasi accented with a circle, similar to the copyright symbol.
|
Command
|
Result
|
|
\textcircled{w}
|
w⃝
|
|
\Large \textcircled{\normalsize\protect\raisebox{-1.5pt}{W}}
|
\Large \normalsize\protectW⃝
|
One has to take care that the character fits in the circle. \Large specifies thereby the size of the circle. With the help of \raisebox the character can be centered.
16.3 Minuscule Numbers↓
Minuscule numbers are created with the command
\oldstylenums↓. The command can be used in formulas and in TeX-mode. The command scheme is:
\oldstylenums{number}
The command \oldstylenums{0123456789 produces: \oldstylenums0123456789
16.4 Miscellaneous special Characters ↓
The following characters can only be inserted to formulas by using commands:
|
Command
|
Result
|
|
\^
|
^
|
|
\_
|
_
|
|
^ \circ↓
|
○
|
The degree sign ° can nevertheless be directly inserted if the LaTeX-preamble contains the following line:
\DeclareInputtext{176}{\ifmmode^\circ\else\textdegree\fi}
17 Formula Styles ↓
-
There are two different alignment styles:
Centered is the predefined standard
Indented for this the option fleqn must be inserted in the menu Document ▷ Settings under Document Class
When
Indented is used, the indentation can be adjusted with the length
\mathindent↓. Should the distance be 15 mm, the following command line is inserted in the LaTeX-preamble
\setlength{\mathindent}{15mm}
When no length is specified, the predefined value of 30 pt will be used.
-
And two different numbering styles:
Right is the predefined standard
Left for this the option leqno must be inserted in the menu Document ▷ Settings under Document Class
fleqn and leqno can also be used together. In this case both options are inserted, separated by a comma.
The chosen styles are used for all displayed formulas of the document. When both, centered and indented formulas should be created in a document, the style
Centered is used. The indented formulas are then set in a flalign environment, see
18.2.3↓.
18 Multiline Formulas ↓
In LyX multiline formulas are created by pressing
newline-insert newline inside a formula. This creates either an
eqnarray environment that is described in
18.3↓ or, when the option
Use AMS math package in the document settings is selected, an
align environment that is described in
18.2.1↓.
There are other multiline formula environments that can be created via the menu Insert ▷ Math. These environments are described in the following sections.
In all multiline formula environments a new line is created by pressing
newline-insert newline. To add or delete lines, the math toolbar buttons

or

, respectively, or the menu
Edit ▷ Rows & Columns can be used.
18.1.1 Line Separation ↓
There is sometimes not enough space in multiline formulas between the lines:
B2(B2 − 2r2g + 2x20 − 2r2k) + 4x20x2 + 4x0xD
=
-4x2B2 + 4x0xB2
4x2(B2 + x20) + 4x0x(D − B2) + B2(B2 − 2r2g + 2x20 − 2r2k)
=
0
In LaTeX additional line space is specified as optional argument of the new line command. This is not yet possible in LyX, therefore the whole formula must be inserted in TeX-mode. To add in our example space, the command \\[3mm] is inserted at the end of the first line. One gets:
B2(B2 − 2rg2 + 2x02 − 2rk2) + 4x02x2 + 4x0xD
amp; =
amp;-4x2B2 + 4x0xB2
[3mm]4x2(B2 + x02) + 4x0x(D − B2) + B2(B2 − 2rg2 + 2x02 − 2rk2)
amp; =
amp;0
To set the line separation for all lines in a formula, the length
\jot↓ is changed. The definition is:
line separation = 6 pt + \jot. Predefined for
\jot is the value 3 pt. To create 3 mm additional line separation as in the previous example, the command
\setlength{\jot}{3mm+3pt}
is inserted in TeX-mode before the formula. This requires that the LaTeX-package
calc↓ was loaded in LaTeX-preamble with the line
\usepackage{calc}
One gets:
\setlength\jot3mm+3pt
B2(B2 − 2r2g + 2x20 − 2r2k) + 4x20x2 + 4x0xD
=
-4x2B2 + 4x0xB2
4x2(B2 + x20) + 4x0x(D − B2) + B2(B2 − 2r2g + 2x20 − 2r2k)
=
0
\setlength\jot3pt To get back to the predefined distance, \jot is set to the value 3 pt.
18.1.2 Column Separation ↓
Multiline formulas form a matrix. A formula in the eqnarray environment is for example a matrix with three columns. By changing the column separation in this environment, the space beside the relation sign can be changed.
The column separation is specified with the length
\arraycolsep↓ according to:
column separation = 2
\arraycolsep
Thus, the command
\setlength{\arraycolsep}{1cm}
inserted in TeX-mode, sets for all following formulas a column separation of 2 cm. To get back to the predefined distance, \arraycolsep is set to 5 pt.
A formula with 2 cm column separation:
\setlength\arraycolsep1cm
A
=
B
C
≠
A
A formula with the predefined column separation for matrices of 10 pt:
\setlength\arraycolsep5pt
A
=
B
C
≠
A
Long formulas can be typeset using these methods:
-
When one side of the equation is much shorther than the line width, this one is chosen for the left side and the right side is typeset over two lines:
The minus sign at the beginning of the second line does normally not appear as operator because it is the first character of the line. Thus it would not be surrounded by space and could not be distinguished from the fraction bar. To avoid this, 3 pt space was inserted behind the minus sign with the command \hspace.↓
-
When both sides of the equation are too long, the command \lefteqn↓ is used. It is inserted to the first column of the first line and effects that all further insertions overwrite the following columns:
After the insertion of \lefteqn, the cursor is in a purple box that is a bit shifted to the left from the blue one. In this the formula is inserted.
The content of the further lines is inserted to the second or another formula column. The greater the column number where it was inserted, the larger the indentation.
Note the following when using \lefteqn:
-
The formula doesn’t use the full page width. When e. g. the term − B2 is added to the first line in the above example, it would have been outside the page margin. To better use the width, negative space can be inserted at the beginning of the first line.
-
Due to a bug in LyX the cursor cannot be set with the mouse into the first line. One can only set the cursor at the beginning of the line and move it with the arrow keys.
-
Other methods to set long formulas are offered by the environments described in 18.5↓ and 18.6↓.
18.1.4 Multiline Brackets ↓
For brackets spanning multiple lines the following problem occurs:
A
=
sin(x)⎡⎣∞∏R = 1(1)/(R) + ⋯
⋯ + B − D]
The closing bracket is smaller than the opening bracket because brackets with variable size may not span multiple lines.
To set the bracket size for the second line correctly, the first line is ended with
\right.↓ and the second line with
\left.↓. After
\left. the command
\vphantom \prod^
\infty ↓_R=1}↓ is inserted, because the multiplication operator with its limits is the largest symbol in the first line and this should be the size for the bracket in the second line.
The result is this:
A
=
sin(x)⎡⎣∞∏R = 1(1)/(R) + ⋯
∞∏R = 1⋯ + B − D]
18.2 Align Environments
Align environments can be used for every kind of multiline formulas. They are specially useful to set several formulas side by side.
Align environments consist of columns. The odd columns are right aligned, the even ones left aligned. Every line in an Align environment can be numbered.
Align environments are created via the menu Insert ▷ Math. With the menu Edit ▷ Math ▷ Change Formula Type already existing formulas can be converted to Align environments.
To add or delete columns, the math toolbar buttons

or

, respectively, or the menu
Edit ▷ Rows & Columns can be used.
18.2.1 Standard align Environment ↓
This Align environment is created by presssing newline-insert newline in a formula or by the menu Insert ▷ Math ▷ AMS align Environment.
An example for two formulas set side by side, that are created with a four column align environment:
A
= sin(B)
C
= D
C
≠ A
B
≠ D
As it can be seen, the formulas in this environment are placed so as if there would be a
\hfill before the first and after every even column. When the formula style
Indented is used, the formula is set without the
\hfill before the first column.
18.2.2 Alignat Environment↓
The alignat environment has no predefined column separation. It can be inserted manually with the spaces that are described
8↑.
The above example in the alignat environment where 1 cm space was inserted at the beginning of the second formula:
2A
= sin(B)
C
= D
C
≠ A
B
≠ D
Because the column separation can be set separately for every column, this environment is especially suitable to set three and more formulas side by side.
18.2.3 Flalign Environment ↓
In this environment the first two columns are always set as much as possible to the left and the last two ones to the right. An example:
A
= 1
B
= 2
C
= 3
X
= -1
Y
= -2
Z
= 4
By creating a flalign environment with an odd number of columns where an empty TeX-brace is inserted to the last column, several formulas in a document can be set to the left, although the formula style
Centered is used. As example the indented formula
(5↑):
The first two columns contain the formula. To indent it as with the formula style
Indented, 30 pt space was inserted at the beginning of the first column.
18.3 Eqnarray Environment ↓
When this environment has been created, three blue boxes appear. The content of the first box is right aligned, the content of the last one left aligned. The content of the middle box appears centered and a bit smaller, because it is designed to insert there only relation characters.
(ABC)/(D)
(ABC)/(D)
(ABC)/(D)
AB
AB
AB
A
=
A
18.4 Gather Environment↓
This environment consists of only one centered column. Every line can be numbered.
18.5 Multline Environment ↓
The multline environment consists, like the gather environment, of only one column. But the first line is left aligned, the last one right aligned. All other lines are centered. Therefore this environment is suitable for long formulas. As example formula
(8↑) in the multline environment:
In the output only the last (first) line of a multline environment appears numbered when the document numbering is right (left).
With the commands
\shoveright↓ and
\shoveleft↓ a centered line can be right or left aligned, respectively. The commands are used as follows:
\shoveright{line content} and \shoveleft{line content}
The length
\multlinegap↓ specifies the distance of the first line from the left page margin. Predefined is the length 0 pt.
As example the above formula where the command
\setlength{\multlinegap}{2cm}
was inserted in TeX-mode before:
\setlength\multlinegap2cm
\setlength\multlinegap0ptThe second line was left aligned using
\shoveleft.
18.6 Multiline Formula Parts ↓
To display only parts of a formula with multiple lines, one of the following environments are used: aligned, alignedat, gathered or split. They can be inserted via the menu Insert ▷ Math or by using the commands described in this section.
The first three have the same properties as the corresponding multiline formula environments, but it is possible to set further formula parts beside them. An example:
ΔxΔp
≥ (ℏ)/(2)
ΔEΔt
≥ (ℏ)/(2)
⎫⎬⎭ Uncertainty relations
To get this formula, a displayed formula is created where the command
\aligned↓ is inserted. A purple box appears around the blue formula box where now columns and lines can be added. Outside the multiline environment other formula parts can be set, like the brace.
The aligned environment is also suitable for long formulas whose lines are horizontally aligned. Using aligned in a displayed formula has the advantage that the formula number is vertically centered behind the lines. As example formula
(7↑) in the aligned environment:
To use the environments
alignedat,
gathered, or
split, the command
\alignedat,
↓ \gathered↓, or
\split↓ are inserted, respectively. The split environment has the same properties as the aligned environment but it can only have two columns.
18.7 Text in multiline Formulas ↓↓
In the Align environments, and the multline and gather environment, text can be inserted that will appear in a separate line and doesn’t affect the column alignment. To do this, the command
\intertext↓ is used in the following scheme:
\intertext{text}
The text should not be longer than a line because it cannot be hyphenated. As LyX doesn’t yet support
\intertext directly, the text is written as mathematical text.
\intertext must hereby be at the beginning of a line and appears in the output above this line. An example where the text was inserted at the beginning of the second line:
19 Formula Numbering↓↓
Numbered formulas can be created with the menu Insert ▷ Math ▷ Numbered Formula (shortcut Ctrl+Alt N). Existing formulas can be numbered with the menu Edit ▷ Math ▷ Toggle Numbering (shortcut math-number-toggle). The formula number is displayed in LyX behind the formula as number sign in parentheses. The number sign is replaced in the output by the formula number.
When numbering is turned on in multiline formulas, all lines will be numbered. But the numbering can be controlled with the menu Edit ▷ Math ▷ Toggle Numbering of Line (shortcutmath-number-line-toggle) for every line.
Except for inline formulas, all formulas can be numbered with two different styles, see
17↑.
19.2 Cross-References↓
All labeled formulas can be cross-referenced. A label is added by the menu
Insert ▷ Label or the toolbar button
. The cursor must hereby be inside a displayed formula. A dialog pops up displaying the prefix
eq: in a text field. The label is inserted there behind the prefix. The predefined prefix means “equation” and makes it easier to find labels in large documents because it marks it as formula label to divide it from e. g. section labels. To change a label, the menu
Insert ▷ Label is used again.
The name of the label is displayed in LyX within two parentheses behind formula. A formula with a label is always numbered.
Cross-references are inserted via the menu
Insert ▷ Cross-Reference or with the toolbar button

. A formula cross-reference appears in the output as formula number. When in the cross-reference dialog window the format
(<reference>) is chosen, the cross-reference appears in the output as formula number in parentheses.
By right-clicking on a cross-reference in LyX, one jumps to the formula that is referenced.
Here are as examples cross-references to formulas of the following subsections:
The equations
(something↓) and
(17↓) are equivalent. In (
24↓) big Latin letters are used for the numbering in contrary to (
22↓).
When the argument of
\tag contains a box like in
9.4↑, the formula cannot be referenced.
19.3 Subnumbering↓
With the help of the commands \begin{subequations} and \end{subequations} formulas can be subnumbered. Both commands are inserted in TeX-mode.
An example:
\addtocounterequation-1
\endsubequations
To create the example, the following is done:
-
first formula is inserted
-
\addtocounter{equation}{-1} \begin{subequations}↓
is inserted after the first formula
-
second formula is inserted
-
third formula is inserted
-
\end{subequations} is inserted after the third formula
Every formula between the commands
\begin and
\end is subnumbered as a, b,
c, … For multiline formulas every line will be subnumbered. All subnumbered formulas are treated as
one numbered formula. But as every numbered formula increases the counter
equation by one, the command
\addtocounter is needed to decrease it. Otherwise the formulas
(15↑),
(16↑),
(17↑) would be numbered as
(15↑),
(18↓),
(18↓).
By inserting the commands in TeX-mode, a space is created between the first two formulas. To revert this -5 mm vertical space is inserted after the command \begin{subequations}. When the formula style Indented is used, -7 mm space is inserted instead.
Here is an example for a multiline formula where the numbering was turned off for the second line:
\endsubequations
19.4 User-defined Numbering ↓
↓With the standard numbering parentheses are set around the formula number. To replace the parentheses for example by vertical bars, the following line is added to the LaTeX-preamble:
\def\tagform@#1{\maketag@@@{|#1|}}
To use other characters, the vertical bars besides the #1 are replaced by one ore more characters. To get only the formula number the vertical bars are omitted.
When there should be an expression of your choice instead of the consecutive formula number in parentheses behind the formula, the command
\tag↓ is used:
In this example the command
\tag something was inserted to the formula.
When the command
\tag* something is inserted instead, the star prevents the parentheses around the expression:
A + B = C
To restart the formula numbering with new document parts or sections, the following command is used:
\@addtoreset{equation}{part}↓
resp.
\@addtoreset{equation}{section}
To be able to use these commands in TeX-mode, the “@” character has to be made “active” for LaTeX using the command \makeatletter. The command \makeatother reverts this. So the command sequence in TeX-mode is:
\makeatletter
\@addtoreset{equation}{section}
\makeatother
In the LaTeX-preamble \makeatletter and \makeatother can be omitted as they are automatically internally inserted by LyX.
To revert
\@addtoreset, the file
remreset.sty↓ has to be loaded in the LaTeX-preamble with the line
\usepackage{remreset}
Then the command
\@removefromreset↓ can be used with the same scheme as
\@addtoreset.
Sometimes formulas should be numbered in the following form:
(section number.formula number)
The formula number should start with every section with “1”.
For this case there is the command
\numberwithin↓, which is used with the following scheme:
\numberwithin{counter}{sectioning}
Counter denotes what kind of numbering is affected, sectioning denotes what number is before the dot.
Thus in our case the following LaTeX-preamble or TeX-Code line is used:
\numberwithin{equation}{section}
This is the result:
\numberwithinequationsection
To number e. g. tables so that the number of the part is the sectioning,
\numberwithin{table}{part} is used.
To go back to the standard numbering or to prevent this kind of numbering when it is defined by the document class, the following command is inserted as TeX-Code or to the LaTeX-preamble:
\renewcommand{\theequation}{\arabic{equation}}↓
or
\renewcommand{\thetable}{\arabic{table}}
\numberwithin uses internally the command \@addtoreset, described above, that also needs to be reverted.\makeatletter \@removefromresetequationsection \makeatother
19.5 Numbering with Roman Numbers and Letters↓↓
Formulas can also be numbered with Roman numbers and Latin letters. To number for example with small Roman numbers, the command
\renewcommand{\theequation}{\roman{equation}}
is inserted before the formula in TeX-mode.
\renewcommand↓ redefines the predefined command
\theequation to the command
\roman{equation}.
equation is the formula counter. When the command
\the is used as prefix for a counter, the value of the counter is output as Arabic number. When a formula is numbered, LaTeX sets internally the command
\theequation behind the formula.
\roman{equation}↓ outputs the counter as small Roman number.
All formulas behind the command
\renewc
ommand are now numbered Roman. To switch to numbering with big Roman numbers, the command is inserted again, but
\roman is replaced by
\Roman↓. To “number” with small Latin letters there is the command
\alph↓, for big ones there is the command
\Alph↓.
Note: Only maximal 26 formulas can be numbered with Latin letters in one document.
To switch back to the default numbering, insert the command:
\renewcommand{\theequation}{\arabic{equation}}↓
As you see, formulas are numbered serially independent from the numbering style. When then numbering should start with “1” when the style is changed, new equation counters have to be defined. A description about this can be found in the file
Formula-numbering.lyx.
20 Chemical Symbols and Equations ↓↓↓
An example text from chemistry:
The SO2 − 4-ion reacts with two Na + -ions to sodium sulfate (Na2SO4). The chemical equation for this is:
This chemical equation can directly be created as formula. To avoid that the symbols appear italic, everything is highlighted and changed by the shortcut font-roman to the upright font style.
A more convenient way to typeset chemical formulas is to use the command
\ce↓ that is available when the LaTeX-package
mhchem↓ is installed. After inserting
\ce to a formula a new blue box appears where chemical formulas can be inserted in an intuitive way.
|
Command
|
Result
|
|
\ce H2CO3
|
\ceH2CO3
|
|
\ce SO4^2-
|
\ceSO42 −
|
|
\ce (NH4)2S
|
\ce(NH4)2S
|
|
\ce KCr(SO4)2.12H2O
|
\ceKCr(SO4)2.12H2O
|
|
\ce A-B\dbond C\tbond D
|
\ceA − B\dbondC\tbondD
|
|
\ce ^227↓_90 → Th+
|
\ce22790Th +
|
|
\ce CO2 + C <=> 2CO
|
\ceCO2 + C < = > 2CO
|
|
\ce CO2 + C ->[\alpha][\beta] 2CO}
|
\ceCO2 + C − > [α][β]2CO
|
Note: Inserting a formula to a \ce box will lead to LaTeX errors. In this case TeX code has to be used like for \ce{$\mu\hyphen$Cl}: \ceμ\hyphenCl
Using
\ce the command for equation
(26↑) is:
\ce 2Na+ + SO4^2- -> Na2SO4
To create multiline chemical equations first a multiline formula is created as described in
18↑. Afterwards the command
\ce is used in every small blue box of the formula.
(27↓) and
(27↓) are an example of a multi-stage chemical reaction where every equation has its own number.
Besides
\ce the
mhchem package provides the command
\cf↓ that has to be used for special cases. For more information about
\cf and more examples have a look at the documentation of
mhchem,
[6].
21 Diagrams
LyX supports two types of commutative diagrams: amscd and xymatrix that are explained in the following.
21.1 Amscd Diagrams↓
Diagrams of this type visualize relations by vertical and horizontal lines or arrows:
A > > > B > > > C
AAA.VVV
F < < < E < < < D
To get them, the command
\CD↓ is inserted to a formula. A blue box appears with two dashed lines where further commands can be inserted. With
newline-insert newline a new line is created. Horizontal relations are inserted in odd, vertical in even formula lines.
To create the relations there are the following commands:
-
@<<< creates a left arrow, @>>> a right arrow and @= a long equal sign
-
@AAA creates an up arrow, @VVV an down arrow and @| a vertical equal sign
-
@. is a placeholder for non-existent relations
All arrows can be labeled as follows:
-
Is text inserted between the first and second < or >, resp., it is placed above the arrow. When it is inserted between the second and third one, it appears under the arrow.
-
When text for vertical arrows is inserted between the first and second A or V, resp., it is placed left beside the arrow. When it is inserted between the second and third one, it appears right beside the arrow. If the text contains an A or V, these letters must be set into a TeX-brace.
As example a diagram with all possible relations:
A > j > > B > > k > C = F
AmAA.VVVV|
D < < j < E > k > > F = C
The command for this is:
\CD A@>j>>B@>>k>C@=F Ctrl+Return
\CD @AmAA@.@VV\{V → V@| Ctrl+Return
\CD D@<<j<E@>k>>F@=C
21.2 Xymatrix Diagrams↓
To be able to use xymatrices, the LaTeX-package
xypic must be installed. A xymatrix is created by inserting the command
\xymatrix in a formula. Then you are able to add new matrix columns and rows like for normal matrices, see
4↑.
In contrary to amscd diagrams, xymatrices supports diagonal and curved arrows, and much more. All possibilities to create commutative diagrams and decorations are explained in detail in the XY-pic manual that you find in the menu Help ▷ Specific Manuals.
21.3 Feynman Diagrams↓
To be able to use
Feynman-diagrams, the LaTeX-package
feyn must be installed. A
Feynman-diagram is created by inserting the command
\Diagram in a formula. Then you are able to add new matrix columns and rows like for normal matrices, see
4↑.
Examples how to create Feynman-diagrams in LyX is given in the Feynman-diagram manual that you find in the menu Help ▷ Specific Manuals.
22 User-defined Commands↓
Note: The names of user-defined commands and macros may only consist of Latin letters.
22.1 The Command \newcommand ↓↓
Many LaTeX-commands are too long to be used frequently. But it is possible to define with the command \newcommand new shorter commands.
The command scheme of \newcommand is:
\newcommand{new command name}[number of arguments][optional value]
\newcommand{command definition}
Note: Assure that the name of the new command is not already used in your document or by LaTeX-packages that you use. When you for example define the command \le for \Leftarrow, you get an error message because \le is already defined as command for “ ≤ ”.
The number of arguments is an integer in the range 0 - 9 and specifies how many arguments the new command should have. With the optional value a value for an optional argument can be predefined. When this is done, the first argument of the new command is automatically an optional one.
Here are some examples:
-
To define the command \gr for \Longrightarrow, the LaTeX-preamble line is:
\newcommand{\gr}{\Longrightarrow}
-
To define the command \us for \underline, the argument (that should be underlined) must be taken into account. For this the preamble line is:
\newcommand{\us}[1]{\underline{#1}}
The character # acts as argument placeholder, the 1 behind it denotes that it is the placeholder for the first argument.
-
For \framebox one can e. g. define the command \fb:
\newcommand{\fb}[3]{\framebox#1#2{$#3$}}
The two Dollar signs creates the extra formula needed for \framebox, see 9.1↑.
-
To create a new command for \fcolorbox where the color for the box needn’t to be specified, the argument for the color is defined optional:
\newcommand{\cb}[3][white]{\fcolorbox{#2}{#1}{$#3$}}
When the color is not specified when using \cb, the predefined color white will be used.
A test of the new defined commands:
|
Command
|
Result
|
|
A\gr B
|
A⟹B
|
|
\us{ABcd
|
ABcd
|
|
\fb{[2cm] → \{ → \{\int A=B
|
[2cm]∫A = B
|
|
\cb{red → \{\int A=B
|
∫A = B
|
|
\cb[green]\{red → \{\int A=B
|
∫A = B
|
User-defined commands are especially convenient for complex expressions. When you are for example dealing in a document with quadratic equations, the same solution type occurs several times. The general form of a quadratic equation is
0 = λ2 + pλ + q
The general form of the solution is
λ1, 2 = − (p)/(2)±√((p²)/(4) − q)
To define a command for the solution formula where only the three parameters λ, p and q need to be specified and the index of λ can be given optionally, the LaTeX-preamble line is
\newcommand{\qG}[4][1,\,2]{#2_{#1}=-\frac{#3}{2}\pm
\newcommand\sqrt{\frac{#3^{2}}{4}-#4}}
To create with this the solution formula, the command
\qG{\lambda → \{p → \{q is inserted to a formula.
The definition of the new command is unintuitive because one has to know the schemes of all used LaTeX commands, e. g. that a fraction is inserted in LaTeX as \frac{numerator}{denominator}. Furthermore one can easily forget a brace in the definition and cannot see in LyX what the new command is doing. To avoid these problems LyX offers the possibility to use math macros instead of the command \newcommand.
A math macro is created by using the menu
Insert ▷ Math ▷ Macro or the toolbar button

. The math macro toolbar appears together with the following box where the macro is defined:

\newmacroname is the default name of the macro that should be changed to something sensible. The wanted formula is inserted in the first blue box. An argument placeholder is inserted with the command
\#argumentnumber, e. g
\#1 or by using the macro toolbar button

. Argument placeholders are displayed red. Maximum 9 arguments are possible. Optional arguments are created with the toolbar button

. The first non-optional argument can be transformed to an optional one with the toolbar button
. In the second blue box the appearance of the macro in LyX can be defined. Normally you want to see it as it is defined, so the box is kept empty. But when you have created a macro that needs lot of space on the screen, you can insert in the box for example
qG: \#1 , \#2 , \#3, \#4
For the macro only the arguments with the macro name in front of them will then be displayed in LyX, leading to a better overview. The formula appears in the output as defined in the first box.
The appearance of macros in formulas can furthermore be changed for single macros by setting the cursor in the macro and using the menu
View ▷ (Un)fold Math Macro.
To use a macro, the macro name is inserted as command to a formula, in our case
\qG. Our macro looks in LyX like this:

Here is our macro example with the arguments
x,
ln(x) and
B:
x1, 2 = − (ln(x))/(2)±√((ln(x)2)/(4) − B)
LyX offers in the menu Tools ▷ Preferences ▷ Editing ▷ Control different styles to edit macros. To find the style that suits you the most, choose a style and set the cursor in a macro formula to see the difference.
A math macro is transformed internally to a \newcommand command when exporting the document. The created \newcommand command is not placed in the LaTeX-preamble, therefore macros can only be used in formulas that are in the document below the macro definition box.
Math macros can also be directly be created from a \newcommand command. When writing for example the command
\newcommand{\larrow}[2]{\xleftarrow[#2]{#1}}
in LyX as normal text, highlighting it completely and using then the shortcut Ctrl+M, the command will be transformed to a math macro. Using this method you need to be careful that the \newcommand command is typed correctly, otherwise you get a faulty macro leading to LaTeX errors.
Math macros currently yet have the problem that further formulas in macro definitions are handled wrongly. Therefore the example
\fb from
22.1↑ cannot be created as macro.
When the cursor is in a macro definition box, you will see the macro toolbar in LyX:
The macro toolbar contains from left to right the following buttons:
23 Computer Algebra Systems
LyX offers the exchange between mathematical expressions written in LyX’s math editor and external applications or user defined scripts. Currently supported applications are Maple, Mathematica, Maxima and Octave. Note that the set of supported mathematical constructs is limited only to very simple cases.
Write some expression in a formula, go to the Edit ▷ Math ▷ Use Computer Algebra System menu and choose the application you have installed on the computer. After that the result of computation should show on the right side of the expression together with the “=” operator.
Here are few simple examples (with results from Maxima) to show what kind of computations can be performed:
-
(37)/(3)*2 − ∑3i = 1ii = − (22)/(3)
-
(37.0)/(3) = 12.33333333333333
-
∫21sin(x)dx = cos1 − cos2
-
det⎡⎢⎢⎢⎣
1
6
7
2
5
8
3
4
17
⎤⎥⎥⎥⎦ = − 56
-
limx → 0⎛⎝(sin(x))/(x)⎞⎠ = 1
23.2 Keyboard shortcut
Currently there is no keyboard shortcut for calling the algebra applications. One can easily bind a shortcut to the math-extern LyX function (see the LyX Functions manual). One could e. g. bind the Return key inside the math editor. To bind it to Maxima one would use this shortcut definition command:
command-alternatives break-paragraph;math-extern maxima
24.1 Negative Numbers↓
Negative numbers often look ugly in formulas because the minus sign before the number is set with the same length as the minus operator sign. When writing the negative number in normal text, the minus sign appears correctly.
Thus, the problem disappears when converting the minus sign to mathematical text.
An example to visualize the problem:
|
normal text:
|
x = -2
|
|
formula:
|
x = − 2
|
|
solution:
|
x = -2
|
24.2 Comma as decimal Separator↓
In LaTeX a comma inside a formula is used, according to the English convention, as number group separator. So there will be space added behind all commas in formulas.
To avoid this, the comma is highlighted and changed to mathematical text (shortcut math-mode).
To use all formula commas in the document as decimal separator, the file
icomma.sty↓ is loaded with the LaTeX-preamble line
\usepackage{icomma}
24.3 Physical Vectors ↓
Predefined vectors are offered by the LaTeX-package
braket↓ that is loaded with the LaTeX-preamble line
\usepackage{braket}
\ifbraket
The following commands are defined:
|
Command
|
Result
|
|
\Bra{\psi
|
\Braψ
|
|
\Ket{\psi
|
\Ketψ
|
|
\Braket{\psi|\phi
|
\Braketψ|φ
|
The command
\Braket assures that all vertical bars are set in the size of the surrounding brackets:
\Braketφ|J = (3)/(2) , MJ
\else
You need to install the LaTeX-package braket to see the rest of this subsection in the output.
\fi
The effect of
\Braket can also be achieved using the command
\middle, that is described in
5.1.2↑.
24.4 Self-defined Fractions ↓
To define custom commands for fractions, the command
\genfrac↓ is used in the following scheme:
\genfrac{left bracket}{right bracket}{fraction bar thickness}{style}
\genfrac{numerator}{denominator}
The style is a number in the range of 0 - 3.
|
Number
|
Style (Size)
|
|
0
|
display style formula
|
|
1
|
inline formula
|
|
2
|
small
|
|
3
|
tiny
|
When no style is given, the size is adjusted to the surrounding environment like for the command \frac.
When no fraction bar thickness is given, the predefined value of 0.4 pt will be used.
For example, the commands
\dfrac and
\tbinom from
3.2↑ are defined with the commands
\newcommand{\dfrac}[2]{\genfrac{}{}{}{0}{#1}{#2}}
and
\newcommand{\tbinom}[2]{\genfrac{(}{)}{0pt}{1}{#1}{#2}}
To define a fraction where the fraction bar thickness can be given as optional argument, the following line is inserted to the LaTeX-preamble:
\newcommand{\fracS}[3][]{\genfrac{}{}{#1}{}{#2}{#3}}
A test:
Command
\fracS[1mm]\{A → \{B
\fracS[5mm]\{A → \{B
Result
\genfrac1mmAB
\genfrac5mmAB
As one can see, the distance of the numerator and the denominator to the fraction bar is round about three times the bar thickness.
24.5 Canceled Formulas↓
To cancel formulas or formula parts, the LaTeX-package
cancel↓ has to be loaded with the LaTeX-preamble line
\usepackage[samesize]{cancel}
\ifcancel
There are four ways to cancel formulas:
|
Command
|
Result
|
|
\cancel{\int A=B
|
\cancel∫A = B
|
|
\bcancel{\int A=B
|
\bcancel∫A = B
|
|
\xcancel{\int A=B
|
\xcancel∫A = B
|
|
\cancelto{1 → \{\int A=B
|
\cancelto1∫A = B
|
\cancelto is especially suitable to visualize the reduction of fractions within formulas:
((x0 + bB)2)/((1 + b2)\cancelto23) = (x20 + B2 − r2g)/(\cancel1 + b2)
\else
You need to install the LaTeX-package cancel to see the rest of this subsection in the output.
\fi
24.6 Formulas in Section Headings ↓
When formulas are used in section headings, the following has to be taken into account:
When hyperref↓ support is enabled in the document settings dialog under PDF Properties, PDF-bookmarks are created for every section heading in the table of contents. If a section heading contains formulas, they are incorrectly displayed in the bookmark text, because formulas in bookmarks infringe the PDF conventions.
Both problems can be solved by inserting at the end of the section heading a short title with the menu Insert ▷ Short Title. Short titles are used as alternative for multiline section headings to keep the table of contents clearly arranged. Only the short title appears in the table of contents and therefore also in the PDF-bookmark.
When formulas should be used in the table of contents but hyperref is used, one can use the following command in TeX-mode:
\texorpdfstring{part}{alternative}↓
Part is the part of the heading that shouldn’t appear in the PDF-bookmark. This can be characters, formulas, footnotes, but also cross-references. The alternative is used instead of the part for the bookmark.
Here are two example headings:
\boldmath
24.6.1 Heading without formula in table of contents √( − 1) = i
24.6.2 Heading with formula in table of contents\texorpdfstring √( − 1) = i
\unboldmath In the first heading a short title was used, in the second one \texorpdfstring.
To get the same formatting as for the other headings, the complete heading was set into a boldmath environment.
24.7 Formulas in multi-column Text↓
Formulas in multi-column text are often too wide to fit into a column and thus need to be set over the whole page width. This is done by using the LaTeX-package
multicol↓, that is loaded with the LaTeX-preamble line
\usepackage{multicol}
Note herby that the setting Two-column document in the menu Document ▷ Settings under Text Layout must not be selected.
Before the multi-column text the command
\begin{multicols}{column number}
is written in TeX-mode. The column number is a number in the range of 2 - 10. Before the formula the multi-column text is ended by inserting the command
\end{multicols}
in TeX-mode.
Due to the command some space is automatically added before the formula. To revert this, -6 mm vertical space is inserted before the formula. When the formula style Indented is used, -9 mm space is inserted instead.
As example a multi-column text with a displayed formula:
2
Das Spektrum wird fouriertransformiert. Die Fouriertransformation wird verwendet, um die überlagerten Signale (Netzwerk, Lösungsmittel) zu trennen. Nachdem wir die Phasenverschiebung bestimmen konnten, interessiert uns nun das Aussehen des Ausgangssignals. Im Experiment haben wir es mit sehr vielen Teilchen zu tun, so dass man über alle Phasen integrieren muss. Sei nun
S unser normiertes Ausgangssignal und
P die Phasenverteilungsfunktion, so ergibt sich die Beziehung
\endmulticols
2
wobei
S0 das Signal ohne Gradient ist und die Normierungsbedingung
∫∞ − ∞P(φ, t) dφ = 1 gilt. Nun dürfen wir aber nicht den Relaxationsprozess außer Acht lassen. Direkt nach dem
π⁄2 -rf-Puls beginnt sich die Magnetisierung zu entfokussieren, wodurch sich das Signal zusätzlich abschwächt. Diese Abschwächung verläuft exponentiell in Abhängigkeit der so genannten
T2-Zeit.
\endmulticols
24.8 Formulas with Description of Variables↓
To describe variables within a formula, like in formula
(30↓), a 2
×n matrix is used with left aligned columns for the
n used variables. To set the description in a smaller size, before the matrix e. g. the command
\footnotesize is inserted.
When the formula style Indented is used, a \hfill is inserted before and after the matrix to have the same separation of the matrix from the equation and the side margin.
When the formula style
Centered is used, the method described in
18.2.3↑ is used to indent formulas. Formula
(30↓) consists of five columns whereas in the first two columns contain the equation, the third the matrix and the last one an empty TeX-brace.
24.9 Upright small Greek Letters ↓
Most of the math fonts only provide italic small Greek letters. But for symbols of elementary particles like pions and neutrinos, upright Greek letters are needed. The file
upgreek.sty↓ that is loaded with the LaTeX-preamble line
\usepackage{upgreek}
provides them. \ifupgreek They are created when the command for a small Greek letters is started with up. For example the command \uptau creates this: τ
With these commands reactions of elementary particles can be typeset:
π + → μ + + νμ
The upright letters are more bold and wider than the italic ones. They should therefore not be used for units like “µm”.
\else
You need to install the LaTeX-package upgreek to see the rest of this subsection in the output.
\fi
24.10 Text Characters in Formulas ↓
In some cases you might want to insert text characters directly into formulas. When for example the centered dot · is often used in formulas like ν = 5·105 Hz, one would have to insert the command \cdot all the time, because this character is defined in all encodings as text character. But the encoding can be changed by this LaTeX-preamble line:
\Declare Inputtext{183}{\ifmmode\cdot\else\textperiodcentered\fi}
The character encoding (menu Document ▷ Settings ▷ Language) specifies what character appears when a keyboard key is pressed. When the key for the character ’·’ is pressed, internally the command \textperiodcentered is used. But this command is not available in a formula so that you would get LaTeX-errors. With the changed encoding the right command is chosen automatically, depending on if the character was inserted into a formula or not.
The encoding of several characters is saved in definition files. Fore example the encoding latin9 is defined in the file latin9.def that is in the installation folder of LaTeX. Encodings should only be changed via the LaTeX-preamble and not in the definition files. Otherwise own documents could not be edited by other LyX users working on other computers.
Besides the centered dot, in this document the degree sign ° is defined with the following LaTeX-preamble line so that it can directly be inserted to a formula:
\DeclareInputtext{176}{\ifmmode^\circ\else\textdegree\fi}
A Typographic Advice↓
This section is a summary of the most important typographic rules, listed in ISO norms.
-
Physical units are always set upright, no matter if they appear in italic text: 30 km/h
Between the value and the unit is the smallest space, see 8.1↑.
This convention is automatically fulfilled when the command \unittwo is used. When it is entered to a formula, two boxes appear. In the first one the value is inserted, in the second one the unit, and one gets as above: 30 km ⁄ h . Note that \unittwo is not a real LaTeX command but the command \unit[value]{unit}, therefore you cannot use it in TeX code.
-
Percent and perthousand signs are set like physical units:
1,2 ‰ alcohol in blood
-
The degree sign follows directly on the value: 15°, but not when it is used in units: 15 °C
-
In numbers with more than four digits the smallest space is inserted before every third digit to group them: 18 473 588
-
For dimensions like 120×90×40 cm the multiplication sign “×” is used. It is available either via the command \times or via the menu Insert ▷ Special Character ▷ Symbols.
-
Functions with names consisting of several letters are set upright to avoid confusions, see 15.1↑.
-
Indices consisting of several letters, are set upright: Ekin
Components of matrices are set italic: Ĥkl
-
The differentiation/integration operator ’d’, the Euler’s number ’e’ and the imaginary unit ’i’ should be set upright, to avoid mixing them up with other variables.
-
The character that denotes a Fourier transformation is inserted either by the command \mathscr F or via the menu Insert ▷ Special Character ▷ Symbols ▷ Letterlike Symbols: ℱ
B Synonyms↓
Some characters and symbols can be created with several commands. Here is a list of the synonym commands:
|
Command
|
equivalent to
|
|
\ast
|
*
|
|
\choose
|
\binom
|
|
\geq
|
\ge
|
|
\lbrace
|
{
|
|
\lbracket
|
[
|
|
\leftarrow
|
\gets
|
|
\leq
|
\le
|
|
\lor
|
\vee
|
|
\neq
|
\not=
|
|
\slash
|
/
|
|
\vert
|
|
|
|
Command
|
equivalent to
|
|
\backslash
|
\\
|
|
\dasharrow
|
\dashrightarrow
|
|
\land
|
\wedge
|
|
\rbrace
|
}
|
|
\rbracket
|
]
|
|
\rightarrow
|
\to
|
|
\lnot
|
\neg
|
|
\ne
|
\not=
|
|
\owns
|
\ni
|
|
\square
|
\Box
|
|
\Vert
|
\|
|
References
[1] Mittelbach, F. ; Goossens, M.: The LaTeX Companion. Addison Wesley, 2004
[2] Description of LaTeX’s math abilities
[3] Description of AmS-LaTeX
[4] List of all symbols available with LaTeX-packages
[5] Documentation of the LaTeX-package hyperref↓
[6] Documentation of the LaTeX-package mhchem↓
[7] Description of the command \mathclap, described in 10.2↑↓
[8] Duden Band 1. 22. Auflage, Duden 2001
[9] Check list for reviewing manuscripts
Index
Accents: ↑
for one character: ↑
for operators: ↑
for several characters: ↑
in text: ↑
Arrows: ↑
diagonal: ↑
horizontal: ↑
labeled: ↑
vertical: ↑
Binomial coefficients: ↑
Boxes: ↑
as paragraph: ↑
colored: ↑
with frame: ↑
without frame: ↑
Bracket size:
Brackets: ↑
for multiline expressions: ↑
horizontal: ↑
vertical: ↑
Case differentiations: ↑
Chemical characters:
Chemical equations: ↑
Comma: ↑
Commands:
@:
\@addtoreset: ↑
\@removefromreset: ↑
A:
\addtocounter: ↑
\aligned: ↑
\alignedat: ↑
\alph: ↑
\alph@\Alph: ↑
\arabic: ↑, ↑
\arraycolsep: ↑, ↑
\arraystretch: ↑
B:
\big: ↑
\bigl - \bigr: ↑
\bigm: ↑
\binom: ↑
\boldmath: ↑
\boldsymbol: ↑
\boxed: ↑
\brace: ↑
\brack: ↑
C:
\CD: ↑
\cases: ↑
\cdots: ↑
\ce: ↑
\cf: ↑
\cfrac: ↑
\colorbox: ↑
D:
\dbinom: ↑
\dbinom@\DeclareMathOperator: ↑, ↑
\definecolor: ↑
\dfrac: ↑
\displaystyle: ↑, ↑
\dotfill: ↑
\dots: ↑
E:
F:
\fbox: ↑
\fcolorbox: ↑
\frac: ↑
\framebox: ↑
G:
H:
\hdotsfor: ↑
\hfill: ↑
\hphantom: ↑
\hrulefill: ↑
\hspace: ↑, ↑
I:
J:
L:
\ldots: ↑
\left: ↑, ↑, ↑
\lefteqn: ↑
\leftroot: ↑
\lim: ↑
\linewidth: ↑
M:
\makebox: ↑
\mathbin: ↑
\mathclap: ↑, ↑
\mathindent: ↑
\mathop: ↑
\mathsurround: ↑
\mbox: ↑
\middle: ↑
\multlinegap: ↑
N:
\newcommand: ↑
\nicefrac: ↑
\not: ↑
\numberwithin: ↑
O:
\officialeuro: ↑
\oldstylenums: ↑
\overbrace: ↑
\overline: ↑
\overset: ↑, ↑
P:
\parbox: ↑
\phantom: ↑
\prod: ↑
R:
\raisebox: ↑
\renewcommand: ↑, ↑
\right: ↑, ↑, ↑
\roman: ↑
\roman@\Roman: ↑
\root: ↑
\rule: ↑
S:
\setlength: ↑
\shoveleft: ↑
\shoveright: ↑
\sideset: ↑
\smallmatrix: ↑
\split: ↑
\sqrt: ↑
\stackrel: ↑
\subarray: ↑
\substack: ↑
\sum: ↑
T:
\tag: ↑
\tbinom: ↑
\texorpdfstring: ↑
\text: ↑
\textbackslash: ↑
\textcircled: ↑
\textcolor: ↑, ↑
\textvisiblespace: ↑
\tfrac: ↑
U:
\unboldmath: ↑
\underbrace: ↑
\underline: ↑
\underset: ↑, ↑
\unitfrac: ↑
\uproot: ↑
V:
X:
\xleftarrow: ↑
\xrightarrow: ↑
Comparisons|seeRelations: ↑
Cross-references:
Delimiters: ↑
Diagrams:
Feynman: ↑
amscd: ↑
xymatrix: ↑
Ellipses: ↑
Exponents: ↑
Font:
Fonts: ↑
Formula:
bold: ↑
canceled: ↑
colored: ↑
display style: ↑
in multi-column text: ↑
in section headings: ↑
inline: ↑
long: ↑
multiline: ↑
Column separation: ↑
Line separation: ↑
align environment: ↑
alignat environment: ↑
eqnarray environment: ↑
flalign environment: ↑
formula parts: ↑
gather environment: ↑
multline environment: ↑
text: ↑
numbering|seeFormula numbering: ↑
styles: ↑
underlined: ↑
with description of variables: ↑
Formula numbering: ↑
self-defined delimiters: ↑
subnumbering: ↑
user-defined: ↑
with Roman numbers: ↑
with letters: ↑
Fractions: ↑
Frames | seeBoxes: ↑
Functions:
modulo-: ↑
predefined: ↑
self-defined: ↑
Greek letters: ↑
big: ↑
bold: ↑
small: ↑
upright: ↑
Indices: ↑
Integrals: ↑
Isotopes|seeChemical characters: ↑
L@LaTeX-preamble: ↑
Limits: ↑
Lines: ↑
Macros: ↑
Mathematical text: ↑
Matrices: ↑
Minuscule numbers: ↑
Negations: ↑
Numbers:
Operators: ↑
Limits: ↑
big: ↑
binary: ↑
self-defined: ↑
Packages:
braket: ↑
calc: ↑, ↑
cancel: ↑
carlisle: ↑
color: ↑
eurosym: ↑
fixmath: ↑
hyperref: ↑, ↑
icomma: ↑
mhchem: ↑, ↑
multicol: ↑
remreset: ↑
upgreek: ↑
was: ↑, ↑, ↑
Placeholders: ↑
Relations: ↑
Roots: ↑
Space:
besides inline formulas: ↑
horizontal: ↑
predefined: ↑
variable: ↑
Special characters: ↑
Subscripts|seeIndices: ↑
Sums: ↑
Superscripts|seeExponents: ↑
Symbols: ↑
Euro-symbol: ↑
chemical: ↑
mathematical: ↑
miscellaneous: ↑
Synonyms: ↑
T@TeX-braces: ↑
T@TeX-mode: ↑
Text:
colored: ↑
in formulas: ↑, ↑, ↑
Tilde: ↑
Tips: ↑
Typographic advice: ↑
Umlauts: ↑
User-defined commands: ↑
Math macros: ↑
\newcommand: ↑
Vectors: ↑
\@: ↑, ↑
\@°: ↑
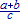
 or by using the menu Insert ▷ TeX Code (shortcut ert-insert).
or by using the menu Insert ▷ TeX Code (shortcut ert-insert).
 , exponents with a caret “^” or via the math toolbar button
, exponents with a caret “^” or via the math toolbar button  .
.
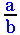 . The font size is adjusted automatically, depending on whether the fraction is in an inline or display style formula. With the math toolbar button
. The font size is adjusted automatically, depending on whether the fraction is in an inline or display style formula. With the math toolbar button  you can select different fraction types.
you can select different fraction types.
 , all other roots with the command \root↓ or with the math toolbar button
, all other roots with the command \root↓ or with the math toolbar button  .
.
 . Analog to fractions (\frac) there are besides \binom the commands \dbinom↓ and \tbinom↓. For other brackets around binomial coeficients there are the commands \brace↓ and \brack↓.
. Analog to fractions (\frac) there are besides \binom the commands \dbinom↓ and \tbinom↓. For other brackets around binomial coeficients there are the commands \brace↓ and \brack↓.
 you can create new lines with the shortcut newline-insert newline or the table toolbar button
you can create new lines with the shortcut newline-insert newline or the table toolbar button  .
.

 that creates one or more phantom characters. When inserting \phantom a small blue box appears that is superposed with two red arrows. The arrows indicate that the complete width and height of the box content will be created as placeholder. Phantom characters are accordingly placeholders with the size of the characters.
that creates one or more phantom characters. When inserting \phantom a small blue box appears that is superposed with two red arrows. The arrows indicate that the complete width and height of the box content will be created as placeholder. Phantom characters are accordingly placeholders with the size of the characters.
 ) and \hphantom↓ (toolbar button
) and \hphantom↓ (toolbar button  ). \hphantom creates only space for the maximal height of the characters in the box but not for its width. \vphantom creates only space for the width of the box content. Therefore the boxes of both commands have only one red arrow.
). \hphantom creates only space for the maximal height of the characters in the box but not for its width. \vphantom creates only space for the width of the box content. Therefore the boxes of both commands have only one red arrow.
 For listings dots at the baseline are used (\ldots↓), while for operations dots are needed that are on the same height as the operators (\cdots↓). When using the command \dots↓, LaTeX decides on the basis of the next character what type is used.
For listings dots at the baseline are used (\ldots↓), while for operations dots are needed that are on the same height as the operators (\cdots↓). When using the command \dots↓, LaTeX decides on the basis of the next character what type is used.
 or the menu Insert ▷ Math ▷ Matrix. In the matrix dialog you can specify the number of columns and rows, the alignment and the decoration. The vertical alignment is hereby only of importance for matrices in inline formulas:
or the menu Insert ▷ Math ▷ Matrix. In the matrix dialog you can specify the number of columns and rows, the alignment and the decoration. The vertical alignment is hereby only of importance for matrices in inline formulas:
 ,
,  , etc. , or the menu Edit ▷ Rows & Columns can be used. New rows can also be created with newline-insert newline.
, etc. , or the menu Edit ▷ Rows & Columns can be used. New rows can also be created with newline-insert newline.
 . Directly behind \left and \right the wanted bracket must be inserted. The bracket size will then automatically be calculated for the output.
. Directly behind \left and \right the wanted bracket must be inserted. The bracket size will then automatically be calculated for the output.
 or the commands listed in the following subsections.
or the commands listed in the following subsections.
 or the commands listed in the following subsections.
or the commands listed in the following subsections.
 or special commands. Independent from the inserted command, one can select the size again by pressing Space afterwards.
or special commands. Independent from the inserted command, one can select the size again by pressing Space afterwards.
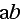 or the menu Edit ▷ Text Style ▷ Customized. The formula number has then the same color as the formula. When the formula number should get another color than the formula characters, the color must be changed within the formula.
or the menu Edit ▷ Text Style ▷ Customized. The formula number has then the same color as the formula. When the formula number should get another color than the formula characters, the color must be changed within the formula.
 .
.
 .
.
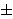 .
.
 can be used.
can be used.
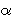 . All international typesetting norms purport that Greek letters in math have to be typeset italic/slanted. In some languages, like French or Russian, they are nevertheless sometimes typeset upright.
. All international typesetting norms purport that Greek letters in math have to be typeset italic/slanted. In some languages, like French or Russian, they are nevertheless sometimes typeset upright.
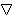 and
and 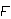 .
.
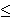 .
.
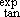 .
.
 .
.
 or
or  , respectively, or the menu Edit ▷ Rows & Columns can be used.
, respectively, or the menu Edit ▷ Rows & Columns can be used.
 or
or  , respectively, or the menu Edit ▷ Rows & Columns can be used.
, respectively, or the menu Edit ▷ Rows & Columns can be used.
 . The cursor must hereby be inside a displayed formula. A dialog pops up displaying the prefix eq: in a text field. The label is inserted there behind the prefix. The predefined prefix means “equation” and makes it easier to find labels in large documents because it marks it as formula label to divide it from e. g. section labels. To change a label, the menu Insert ▷ Label is used again.
. The cursor must hereby be inside a displayed formula. A dialog pops up displaying the prefix eq: in a text field. The label is inserted there behind the prefix. The predefined prefix means “equation” and makes it easier to find labels in large documents because it marks it as formula label to divide it from e. g. section labels. To change a label, the menu Insert ▷ Label is used again.
 . A formula cross-reference appears in the output as formula number. When in the cross-reference dialog window the format (<reference>) is chosen, the cross-reference appears in the output as formula number in parentheses.
. A formula cross-reference appears in the output as formula number. When in the cross-reference dialog window the format (<reference>) is chosen, the cross-reference appears in the output as formula number in parentheses. . The math macro toolbar appears together with the following box where the macro is defined:
. The math macro toolbar appears together with the following box where the macro is defined:
 . Argument placeholders are displayed red. Maximum 9 arguments are possible. Optional arguments are created with the toolbar button
. Argument placeholders are displayed red. Maximum 9 arguments are possible. Optional arguments are created with the toolbar button  . The first non-optional argument can be transformed to an optional one with the toolbar button
. The first non-optional argument can be transformed to an optional one with the toolbar button  . In the second blue box the appearance of the macro in LyX can be defined. Normally you want to see it as it is defined, so the box is kept empty. But when you have created a macro that needs lot of space on the screen, you can insert in the box for example
. In the second blue box the appearance of the macro in LyX can be defined. Normally you want to see it as it is defined, so the box is kept empty. But when you have created a macro that needs lot of space on the screen, you can insert in the box for example